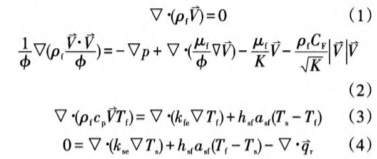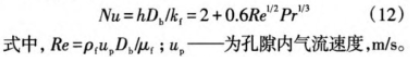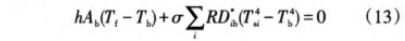高溫多孔材料中氣流溫度的熱電偶測量誤差

摘要:通過對熱電偶結點傳熱的數值模擬,研究高溫多孔材料內氣流溫度的測量誤差。首先采用局部非熱平衡模型和蒙特卡羅法求解管內多孔材料的輻射對流耦合換熱,獲得速度場和溫度場;根據所得速度場和溫度場,基于能量平衡建立熱電偶結點的傳熱模型。再次利用蒙特卡羅法求解熱電偶結點與周圍多孔骨架的輻射換熱，進而計算結點溫度。針對管壁等溫條件，分析穩態測量時熱電偶結點溫度與當地氣流溫度的差異，討論管壁溫度、氣流速度、結點發射率和結點尺寸的影響。結果表明,管壁溫度越高,氣流溫度測量誤差越大，管壁溫度1500K時的最大誤差為10.4%;氣流人口速度增大,結點溫度相對于氣流溫度的偏離程度減小,偏離峰值出現在無量綱管徑r/R=0.6-~0.8范圍內;減小結點尺寸和降低結點表面發射率可有效減小測溫誤差。
0引言
　　熱電偶測溫已廣泛應用于工業生產和科學研究;在對流體溫度測量時,由于存在裝配誤差、傳熱誤差和動態響應誤差等,熱電偶示值與流體真實溫度存在差異"。針對傳熱誤差的分析和修正，國內外學者已經展開大量研究[2.31。多孔材料在傳熱領域具有廣泛應用前景,如太陽集熱器和相變儲熱等(4.5)。在其流動換熱實驗研究中也常采用熱電偶對其中流體相溫度進行測量。一些學者認為測溫位置處于局部熱平衡,從而用熱電偶直接表征流體相和固相溫度'。僅部分學者考慮流、固兩相溫差即局部非熱平衡,分別對固相和流體進行測溫;Lee等[")通過直徑25μm的熱電偶測量蜂窩多孔陶瓷燃燒器內氣相溫度;Zheng等']使用成對布置的裸露與包覆熱電偶測量多孔燃燒器內固相(氧化鋁小球)和氣相溫度;Dukhan等[9)采用開孔套管熱電偶組件對泡沫金屬內氣流溫度進行測量。然而,針對高溫多孔材料內熱電偶測溫誤差的分析還比較缺乏。Zheng等[8]通過建立熱電偶傳熱模型獲得氣相的修正溫度,采用平均固相溫度對結點與周圍固相環境的輻射換熱進行了簡化。
　　輻射換熱對熱電偶高溫測量產生的影響較大,由于熱電偶結點尺寸相對較小,大多文獻對結點的輻射換熱簡化處理,即小尺寸結點與大封閉空間的輻射換熱[0)。然而,三維網狀多孔材料的孔隙尺寸與熱電偶結點尺寸量級相當，結點與周圍固體骨架進行輻射換熱,熱電偶的測量誤差受結點接收和發射輻射的綜合影響。此時,采用該簡化處理無法準確預測熱電偶測溫的輻射影響。本文通過數值模擬的方式對多孔材料內熱電偶的測溫誤差進行分析;采用蒙特卡羅法求解熱電偶結點與多孔骨架的輻射換熱,分析氣流速度、結點尺寸和結點表面發射率等參數的影響。
1多孔材料耦合換熱計算
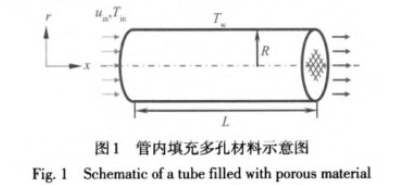
　　通過數值模擬獲得多孔材料內速度場和溫度場,將其作為熱電偶測溫誤差分析的已知條件。如圖1所示,本文以填充多孔材料的等壁溫圓管內流動換熱為計算模型。多孔材料視為吸收、發射、各.向同性散射灰體,流體為非參與性介質,利用蒙特卡羅法求解固相骨架的輻射換熱;流動為不可壓縮穩定層流,采用Brinkman-Forchheimer擴展達西模型描述。基于局部非熱平衡模型，基本控制方程胃：
 
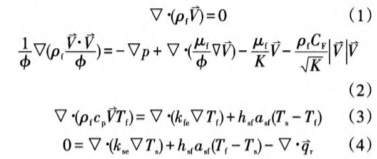
　　式中,pf--流體密度,kg/m';`V一-達西速度,m/s;φ--多孔材料的孔隙率;p一流體壓力，Pa;μf-一動力粘度,kg/(m.s);K-多孔材料的滲透率,m²;CF--Forchheimer系數;cp一流體比熱容,J/(kg.K);T-溫度,K;kfe和kne一流體和骨架的有效導熱系數，W/(m.K),本文采用Kfe=φkf,,ks_=(-中)k,,其中k為流體的導熱系數，W/(m.K),k,為骨架材質的導熱系數，W/(m.K);h,--多孔材料流、固兩相界面的對流換熱系數,W/(m².K);atp-比面積,m<sup>-1</sup>;`q,-輻射熱流，W/m²;下標f、s-流體、固體。
 
　　利用蒙特卡羅法求解輻射換熱問題已得到大量研究,其基本原理見文獻[11]。利用歸一化的輻射傳遞系數RD*tf;及其倒易關系,式(4)中輻射換熱源項對離散單元△Vj可表示為:
 
 
2熱電偶傳熱模型
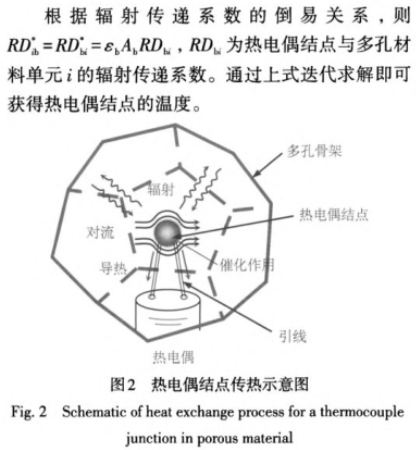
　　當熱電偶置于被測氣流中，熱電偶結點的熱平衡建立基于對流換熱、引線導熱、輻射換熱和催化反應熱(如圖2所示);其中，引線導熱影響可通過合理選擇引線尺寸和控制浸人長度等方式減小,催化反應熱可通過涂層產生隔離作用予以減少或避免1。高溫測量時,輻射影響比重很大,分析中可忽略引線導熱和催化反應熱的影響(:16]。采用集中參數法,熱電偶結點的穩態傳熱方程可表示為:
 
　　式中,Qev和Qt一熱電偶結點與氣流的對流換熱量和與多孔骨架的輻射換熱量,W;Ab-熱電偶結點表面積,m²;T,-熱電偶結點溫度,K;ab,和εb,一分別為結點表面吸收率和發射率;Gb一-多孔骨架對結點表面的投人輻射,W/m²;h一-.氣流與熱電偶結點的對流換熱系數，W/(m².K),結點可看作直徑為Db的球體,努塞爾數Nu采用經驗公式"]:
 
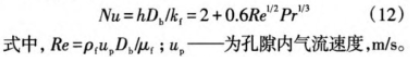
　　采用蒙特卡羅法對熱電偶結點與周圍骨架的輻射換熱進行求解,多孔材料仍視為吸收散射性介質,引入歸--化輻射傳遞系數RD*ab,式(11)可改寫為:
 
 
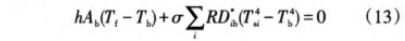
3結果分析
　　本文基本計算參數:R=0.05m,L=1.0m;uim=1.0m/s,Tin=300K;ρt=1.205kg/m³',cp=1005J/(kg.K),k,=0.0259W/(m.K),μf=1.81x10^-5kg/(m.s);ps=3200kg/m³,cs=750J/(kg.K),ks=80W/Km-K);φ=0.9,dp=2.54mm,ε=0.92;Db=1.0mm,εb,=1.0;管壁為黑體(εw=1.0),Tw=1000K。由于多孔材料的容積換熱性能很強,多孔材料的流、固兩相溫差沿軸向逐漸減小，最終達到熱平衡,這時熱電偶結點溫度即可表征流體/固體溫度[(]。本文重點針對局部非熱平衡區域內(即氣、固兩相存在溫差)的氣流溫度測量進行詳細討論。
3.1計算可靠性分析
　　蒙特卡羅法計算耦合傳熱已得到本課題組充分驗證""。針對多孔材料內的流動換熱,圖3為不考慮輻射效應采用局部非平衡模型模擬等壁溫圓管內流、固兩相溫度的結果。基本參數為:
 
3.2管壁溫度影響
　　管壁溫度Tw為800、1000、1500K時,熱電偶結點溫度計算結果見圖4,其他參數保持不變。3個管壁溫度下，x/R=1.9位置的徑向氣流溫度測量最大誤差分別為16.7K(2.8%).35.8K(5.1%)和111.0K(10.4%);x/R=3.9時分別為8.7K、16.7K和30.7K。由于多孔材料容積換熱系數很大,氣固兩相溫差沿軸向逐漸變小,最終達到局部熱平衡,
 
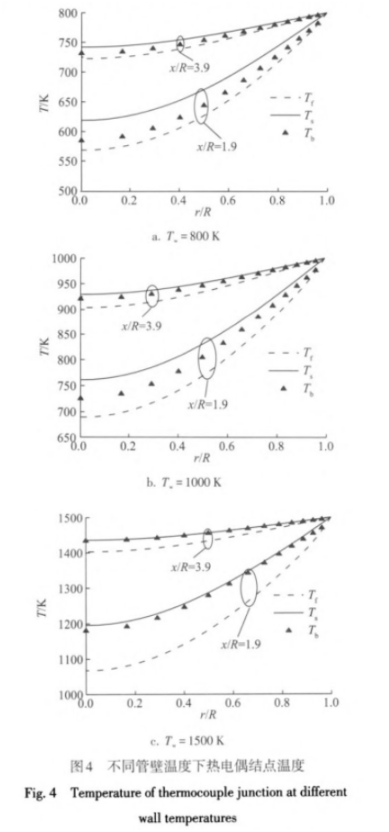
　　即誤差沿軸向逐漸減小。熱電偶結點溫度處于兩相溫度之間,管壁溫度越高，氣固兩相溫度也增高，多孔骨架輻射的影響增大,從而熱電偶結點溫度越接近固相溫度。另外,在管內核心區的測溫誤差較大,越靠近管壁,氣固溫差減小,結點溫度與氣流溫度偏差也減小。
3.3流速影響
　　圖5為氣流入口速度uin為0.5.1.0、1.5m/s時，x/R=1.9位置徑向熱電偶結點溫度與當地氣流溫度的對比曲線,其他參數保持不變。可以看出,人口流速減小，同一截面上氣固兩相溫度都有所增高;而溫度測點位置的局部流速小，導致結點對流換熱減弱,熱電偶結點溫度偏離氣流溫度的程度增大。結合氣固兩相溫度分析,由圖5b可知,在管徑r/R=0.6~0.8范圍內出現偏離峰值。.
 
3.4熱電偶結點參數影響
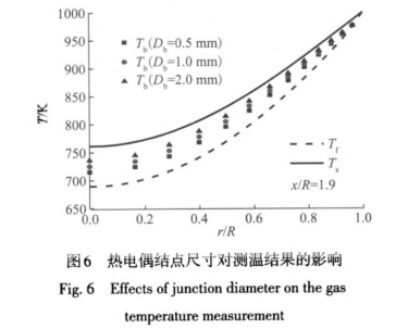
　　圖6為熱電偶結點尺寸對多孔材料內氣流測溫的影響。可見,熱電偶尺寸越大,對流換熱減弱，輻射換熱的影響相對增大,熱電偶結點溫度相對于氣流溫度偏差越大。如結點直徑Db=2.0mm時最大誤差為46.4K;D,=0.5mm時為26.2K。
 
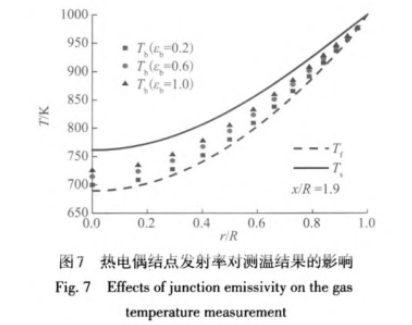
　　熱電偶結點表面發射率對氣流測溫的影響如圖7所示。熱電偶結點發射率越大,結點與測點周圍多孔骨架的輻射換熱越強,結點溫度越接近固相溫度,與氣流溫度偏差越大。如結點發射率εb=1.0時最大誤差為35.8K;εb=0.2時為10.4K。由此可知,采用小尺寸和低發射率的熱電偶結點可減小多孔材料內氣流溫度的測量誤差。
 
4結論
1)管壁溫度越高,多孔材料內氣固兩相的溫度越高,熱電偶測量氣流溫度的誤差越大,熱電偶結點溫度越接近固相溫度;如管壁溫度1500K時，x/R=1.9位置氣流溫度最大測量誤差為111.0K(10.4%)。
2)氣流入口速度增大,溫度測量位置處的結點對流換熱增強,熱電偶結點溫度相對于當地氣流溫度的偏離程度減小;如速度0.5m/s時最大偏離程度為0.69;速度1.5m/s時為0.57。偏離峰值出現在無量綱管徑r/R=0.6~0.8范圍內。
3)熱電偶結點尺寸和發射率對測溫誤差有較大影響。結點尺寸越小,對流換熱增強,輻射影響相對減小;發射率減小,輻射換熱影響減小。如結點直徑由2.0mm減至0.5mm時,最大測量誤差由46.4K變為26.2K;結點發射率由1.0降低至0.2.時,最大誤差由35.8K變為10.4K。可見,減小結點尺寸和降低結點表面發射率均可有效減小高溫多孔材料內氣流溫度的測量誤差。