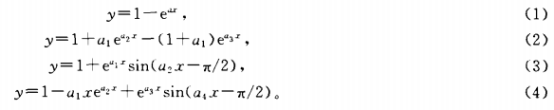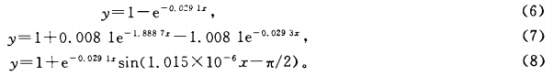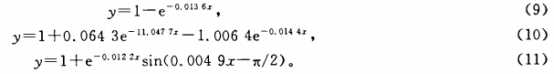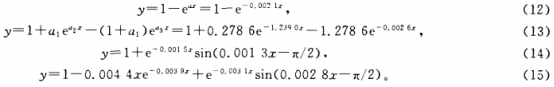熱電阻的動態響應特性

摘要:熱電阻是最普遍使用的測溫元件之一,工程中一般給出熱電阻測量的滯后時間,而對測量的過渡過程缺乏深入的分析。以WZP1500型、WZP120型和有導熱油的WZP120型Pt100熱電阻為例,研究了它們的過渡過程。通過對實驗數據的分析綜合、參數辨識,得到了它們的階躍時間響應函數和傳遞函數。同時,對影響熱電阻數學模型結構的因素、影響數學模型參數大小的因素進行了分析,得到的結論可用于新熱電阻數學模型的建立。
　　熱電阻是使用最普遍的測溫元件,在溫度測量中,熱電阻響應的滯后給系統的測量和控制帶來了很多麻煩。工程中一般給出熱電阻的滯后時間,即傳熱系統達到穩定的調整時間,而對從干擾出現到系統穩定的過渡過程缺乏深人的分析。隨著熱動力學研究的深人開展,傳熱的動態過程越來越受到人們的重視。在傳熱的動態控制和高效傳熱設備的研究中,建立數學模型有著現實的意義。
　　Pt100鉑熱電阻在工程中使用得非常普遍,通常裝有保護套管。例如:在反應釜中,為了保護熱電阻,常將熱電阻放在裝有導熱油的銅管中,這種情況下,熱電阻測量的滯后更為嚴重。對WZP1500型(裝有φ8保護套管)、WZP120型(裝有φ16保護套管)和WZP120型熱電阻(插人φ50mm的紫銅管子中的導熱油中)測量溫度的3種情況的瞬態響應特性進行了研究。通過對實驗數據的分析綜合、參數辨識，得到了它們的階躍時間響應函數和傳遞函數。實驗表明,不同型號熱電阻過渡過程的動態特性有較大的差別。對于熱容性滯后較大的熱電阻，不能作為一階系統處理,而應采用高階系統或有滯后環節的系統來處理。
1實驗、時域響應與參數辨識
1.1實驗與階躍響應的參數識別
　　通過實驗檢測熱電阻在過渡過程中的動態響應,實驗中,分別將3種實驗用的熱電阻從常溫水中迅速置于沸騰水中,給熱電阻一個階躍輸人變化，記錄熱電阻的輸出數據,即熱電阻的溫度指示值。溫度數據的采集,經熱電阻變送器,再經A/D轉換,變成數字信號后由計算機數據采集系統自動完成。
　　熱電阻與測量流體接觸的滯流層、熱電阻內部的導熱油以及空氣夾層對數學模型都有影響。為了得到簡單實用的數學模型,假設熱電阻的階躍動態響應為如下結構。
 
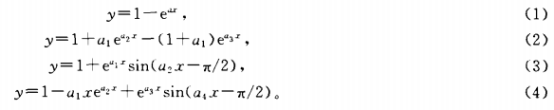
　　式(1)和式(2)表示了一階和二階系統的階躍響應.式(3)和式(4)用sin(ux-π/2)因子對一階和二階模型進行了修正,為的是表示熱電阻中存在的純延遲特性。純延遲特性是由于熱電阻材料和導熱油等的熱容引起的,這一點在后面的實驗數據曲線中可以看出。
　　確定階躍動態響應的結構時,函數應該滿足2個條件:在x=0時,y=0;x-→∞時,y→1。顯然,上面假設的數學模型的結構滿足這2個條件。這些數學模型中，含有未知參數,這些參數可以根據實驗數據作參數辨識時得到。
　　為了得到通用的結果,整理實驗數據時,將得到的實驗數據歸一標準化。
 
　　式中:x是歸一化時間,代表階躍信號加入的時間,單位是s;t0是階躍信號加人的時刻;4;是對應溫度T;的時刻;T0是熱電阻的初始溫度;Tmax是傳熱穩定后熱電阻的指示溫度;T;是當前時刻熱電阻指示的溫度;y是歸一化的溫度值。
　　曲線擬合在MATLAB平臺上進行[2],借助fminsearch指令對未知參數進行的非線性最小二乘估計,得到如下的數學模型。
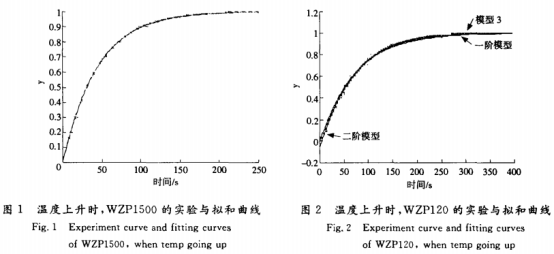
　　對于WZP1500型熱電阻,采用一階數學模型、二階數學模型和用sin(ux-π/2)修正的一階數學模型擬和實驗曲線,得到的階躍響應是:
 
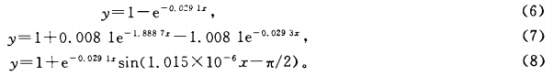
　　圖1中的實線表示了3個方程的曲線,它們與實驗曲線都吻合得較好,但是--階數學模型是最簡單的。因此，可以用一階數學模型代表WZP1500型的熱電阻。
　　同樣,對WZP120型的熱電阻采用一階數學模型、二階數學模型和用sin(ax-π/2)修正的一階數學模型擬和實驗曲線,得到的階躍響應是:
 
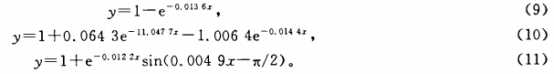
　　圖2中的實線表示了3個方程的曲線,其中二階數學模型的曲線在開始時刻有較大的誤差,而且二階數學模型有3個參數,結構相對復雜。WZP120型的熱電阻的實驗曲線在開始部分有純延遲存在,修正的一階數學模型比一階數學模型更能體現這--特性。因此,用修正的一階數學模型代表WZP120型的熱電阻更合理些。
 
　　油浸的WZP120型的熱電阻具有較長的延遲時間,這可從圖3的實驗數據曲線看出。采用一階數學模型、二階數學模型、用sin(ar-π/2)修正的一階數學模型和用sin(ux-π/2)修正的二階數學模型擬和實驗曲線,得到的階躍響應是:
 
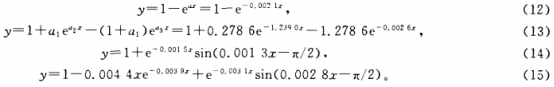
　　很明顯,由于大的時間延遲存在,前3種數學模型都有很大的誤差,只有用sin(ax-π/2)修正的二階數學模型比較好的擬和了實驗曲線，因此,可以用這一個數學模型表示它的特性。如果用更高階的數學模型會有更好的逼近,但增加了模型的復雜性。
1.2階躍響應函數的分析
　　WZP1500型熱電阻由于套管直徑只有8mm,熱容性滯后很小,所以3種數學模型的誤差都很小。修正后的一階數學模型精度更高些,但是一階數學模型是最簡單的，因此更具有實用性。
　　對于WZP120型熱電阻,套管直徑是16mm,有明顯的熱容性滯后,這可以從實驗曲線開始有1個平坦段看出。當熱電阻受到溫度突變的階躍激勵時,熱電阻保護套管首先要預熱,而后熱電阻才能感應到溫度的變化。因此,3種數學模型有較明顯的差別。sin(ax-π/2)因子具有修正時間滯后的作用,用sin(ax-π/2)修正的一階數學模型具有較高的精度。
　　油浸WZP120型中,由于導熱油的存在，只有在導熱油被加熱后,熱電阻才會有響應,因此,造成了較大的熱容性延遲。該系統具有純滯后特性,純滯后的時間大約為150s。在數學模型中,這是不可忽視的因素。用sin(ax-π/2)因子修正的二階模型是最簡單的,但在初始階段,存在不合理的估計值。實際使用時,對于響應為負值的數據可處理為0,作為處理純延遲的方法。要想得到更高的精度,只有采用更復雜的模型,如采用sin(ax-π/2)修正的三階數學模型。
　　因此,對于熱容性滯后小的熱電阻、熱容性滯后較大的熱電阻和熱容性滯后很大的熱電阻的數學模型的結構分別是:
 
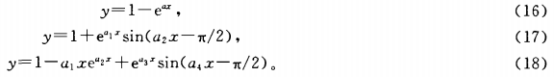
　　值得說明的是,對于同一個熱電阻，其數學模型的結構是相同的,但參數不同。圖4~圖6比較了同一個熱電阻在升溫和降溫時的階躍響應,可以清楚地看出復合材料傳熱的不對稱性[2],即熱電阻的傳遞函數具有相同的結構,但參數不同。
 
 
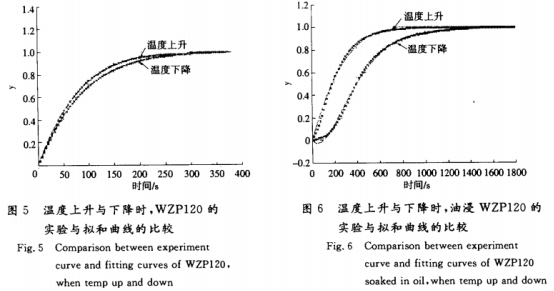
2傳遞函數
　　在設計傳熱控制系統時,使用時域響應函數是不方便的,通用的方法是用傳遞函數設計控制系統。對于上面的3種熱電阻數學模型的傳遞函數,求出它們輸出和輸人函數的拉普拉斯變換,進而即可求得它們的傳遞函數。
　　一階數學模型輸出的拉氏變換是:
 
　　這都是很標準的拉普拉斯變換形式,其反變換很容易從數學手冊中查到。由于傳遞函數是系統本身的性質,所以得到的傳遞函數具有通用性。
3結論
1)熱電阻的數學模型可用一階系統、二階系統、修正的一階系統或修正的二階系統表示;
2)熱電阻熱容引起的容性時間滯后對數學模型有關鍵的影響,熱容越大,數學模型的階數越高;
3)熱電阻數學模型中,通過增加[sin(ax-π/2)]因子,可以較好的模擬時間滯后的影響;
4)使用條件相同時,同一熱電阻的數學模型的結構具有不變性,但模型中的參數與熱電阻的邊界條件有密切的關系,即在不同的介質中,熱電阻的傳遞函數的結構相同,但具有不同參數;
5)在同一種介質中,測量升溫和降溫時，同一熱電阻數學模型的結構是相同的,但參數不同,即傳熱具有不對稱性。