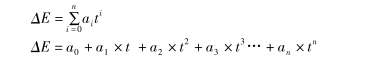熱電偶偏差熱電勢曲線擬合的研究
發布時間:2022-12-01
瀏覽次數:
摘要:針對
R型熱電偶在6個IIS90溫標溫度點的偏差熱電勢分別用最小二乘法和切比雪夫法進行了多階曲線擬合并用CurveExpert軟件驗證了擬合系數的正確性給出了多階函數的擬合公式。
《R型熱電偶內插公式的分析與研究》論文中闡述了在測量R型熱電偶6個固定點上的分度熱電勢mV值后如何計算未知溫度點的偏差熱電勢值的擬合方法進行了討論并給出了偏差電勢和內插公式。論文針對上述測量數據應用RADStudio軟件開發出最小二乘法和切比雪夫法實現熱電偶偏差熱電勢曲線擬合的工程軟件并應用CurveExpert曲線軟件對計算結果進行驗證。
1測量模型
熱電偶的國際溫標ITS-90由NIST美國國家標準與技術研究院在1993年發布
熱電偶的參考熱電勢計算公式為:

公式中Eref為ITS-90溫標的標準參考熱電勢值△E為偏差熱電勢值。△E的數值如何確定直接關系到熱電偶傳感器在任意溫度點的熱電勢求解。同(R型熱電偶內插公式的分析與研究》論文所述-樣建立偏差熱電勢與溫度的擬合公式測量模型。
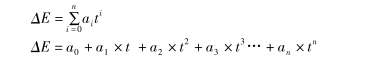
依據表1在6個固定點有6個熱電勢插值與之對應。研究過程就是需要對這些離散的數據點集進行擬合使得擬合的曲線盡量多的穿過所給出的離散點并且.誤差值盡可能小。從而通過擬合的函數找出離散點的計算規律,以此推斷出任意溫度點的熱電勢偏差值。
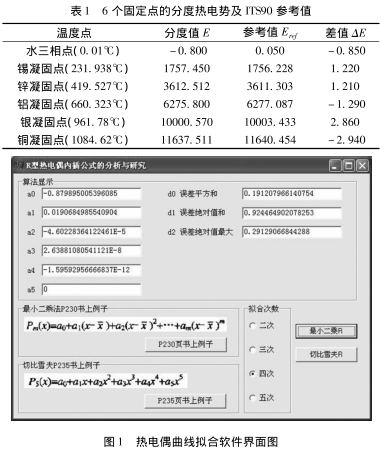
最小二乘法的計算標準是使求得的擬合函數與給出的實際離散點之間的誤差平方和最小。而切比雪夫法的計算標準是使求得的擬合函數與給出的實際離散點之間的誤差最大值為最小。為了便于對比計算,課題應用RADStudio軟件可發出針對兩種擬合方法在不同階次的擬合計算軟件,同時多設置3個變量分別表征d0誤差平方和、d1誤差絕對值和、d2誤差絕對值最大值。下圖1為.軟件的程序界面。CurveExpert1.4是-款專業的曲線擬合軟件如圖2所示,通過它能快速的分析出給定數據最適合何種曲線并推算其函數方程式并及給出數據的標準誤差及相關系數,課題應用CurveExpert軟件對曲線擬合軟件的數據運算進行驗證,以確保多階曲線擬合的正確性。

2擬合計算
最小二乘法和切比雪夫擬合算法計算針對20階以內的數據擬合有效對于熱電偶的數據擬合而言,已經足.以滿足計算要求標定的數據點一般為6個,曲線擬合n值為1至5。
2.1最小二乘法
n=5時課題擬合計算結果如下但是CurveExpert軟件提示6個數據點并不滿足5次的曲線擬合要求,因此不采用此組擬合曲線參數。
a0=-0.850041998463831
al=0.00419920929112408
a2=6.37116245722718E-5
a3=-2.44436511901853E-7
a4=2.70582418257385E-10
a5=-9.60481199754648E-14

n=4時擬合曲線的系數如下所示與圖3所示的CurveExpert擬合系數對比驗證系數完全一致達到預期計算效果同樣n為3和2時的計算系數經驗證也完全一致。
a0=-0.879895005396085
al=0.0190684985540904
a2=-4.60228364122461E-5
a3=2.63881080541121E-8
a4=-1.59592956666837E-12n=3時
a0=-0.874781128095732
al=0.0186127951094208
a2=-4.37481584610491E-5
a3=.2.29522241448483E-8
n=2時
a0=-0.27389292847006
al=0.00486367370529746
a2=-7.29961208590609E-6
3.2切比雪夫法
切比雪夫曲線擬合的系數如下
n=5時
a0=-I.0570321937135
al=0.020123509226792
a2=-4.57805634220434E-5
a3=2.19960749682939E-8
a4=1.65323650831879E-12
a5=0.206830963199262
n=4時
a0=-1.0570321937135
al=0.020123509226792
a2=-4.57805634220434E-5
a3=2.19960749682939E-8
a4=.1.65323650831879E-12
n=3時
a0=-1.06379901987901
al=0.0204501360801971
a2=-4.75657684751315E-5
a3=2.50891732556674E-8
n=2時
a0=-0.0138754403562611
al=0.00369513844519069
a2=-6.60498430353681E-6
3結論
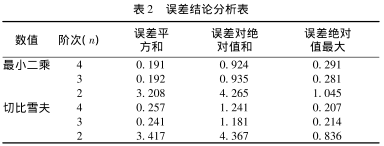
將上述兩種方法求得的擬合曲線分別帶入6個固定點數值得出表2所示的誤差結論分析表。
為了便于查看保留3位有效數字很容易的可以看出最小二乘法n=4時6個固定點的誤差平方和最小;切比雪夫法n=4時6個固定點的誤差絕對值最大值最小。階次越大曲線擬合的效果越好越能滿足熱電偶在不同溫度點的熱電勢偏差值計算要求。