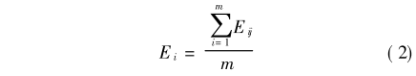熱電偶布置方式對測溫結果的影響

摘要:利用熱電偶并聯理論，對不均勻溫度場進行了分析。利用數據采集板PCL-818HG對熱電偶的熱電勢信號進行處理,用VisualBasi:編寫控制程序，實現了溫度信號的數字化采集和顯示。分析了準穩態法測導熱系數實驗過程，在熱源相互干擾的不均勻溫度場條件下，比較多支熱電偶單點布置方式與并聯布置方式的優缺點，得出了利用熱電偶并聯對不均勻溫度場測量的參考式，并對該實驗進行了改進。
1引言
　　在用準穩態法測平板導熱系數的傳熱實驗中心2，實驗平板上下表面的中心各布置了一對熱電偶，在實驗過程中發現平板表面溫度是不均勻的，使得測量計算的結果誤差較大。可采用多點測量并取平均值的方法來改進。為進一步減少多點測量占用通道數目過多的弊端，可將多對熱電偶并聯，既能提高測量的精度，又能避免占用通道過多的矛盾，效果明顯。
2溫度信號的數字化采集系統.
　　溫度測量使用自制的T型熱電偶，線徑為0.2mm,并進行了標定。數采板采用PCL-818HG,通過硬件設置使其16個單通道工作在差模狀態下3。利用VisualBasie語言編寫控制程序同時顯.示8組數據，并且能夠實現數據的記錄以及采樣頻率的設置。程序可以對8個通道進行實時數據監控，并將采集到的數據轉換成溫度信號。程序啟動后，隨即生成一個txt文件，溫度數據被保存在該文件下，便于數據處理。
3單點與并聯布置方式的測溫結果分析
　　在厚度為0.015m的正方形平板實驗塊表面,等面積地布置6對熱電偶，當溫度場達到平衡狀態時，測量出這6個點的溫度，而這6對熱電偶所產生的平均熱電勢Ep可視為基準值，因為Ep可以看作相對高一級儀表測量得到的值，可看作真值(也稱相對真值)。以這6對熱電偶為中心將正方形實驗塊平分為6個正方形小面積作為微分單元，截面.上的平均熱電勢Ep為國:
 
　　其中Ei是指第i個熱電偶m次測量的平均熱電勢;Si是指第i個熱電偶所占的正方形小格面積;S是指整個平板的面積。據公式(1)，計算上述單點布置條件下溫度的平均值以及平均溫差和導熱系數的值。對于第i支獨立的熱電偶，測量m次，再求出其平均熱電勢:
 
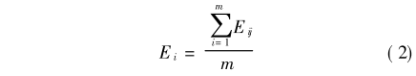
　　在PC機上運行采集程序，將采樣頻率設置成為30s通過實驗測得數據并利用上述理論計算,得出曲線如圖1所示
 
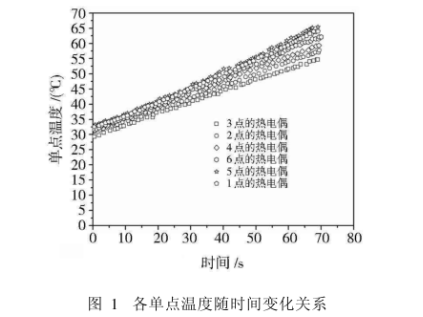
　　可以看出，隨著時間的推移，溫度場的不均勻程度在逐漸增加。這樣不同的點計算出的物體的導熱系數肯定會有差異，為減小這種差異，可計算表面的平均溫度。利用上述理論計算方法，運用微分的思想，來計算表面上的平均溫度，如圖2所示。同時，布置6個并聯熱電偶繼續從頭開始測量，電源為50V，平板及加熱器初始溫度為室溫，數據采集板的采樣頻率設置為30$初始溫度相同時開始記錄新數據，保持初始過余溫度相同，測量結果也一并繪制在圖2中。
 
　　由以上數據可以得出如下結論:(1)熱電偶并聯值與單點溫度平均值基本吻合;(2)在一定溫度范圍內溫度場的平均值是并聯值的線性函數;(3)通過實驗證明，并聯熱電偶可以準確測量不均勻溫度場的平均溫度，與理論相吻合。
4理論應用
　　先做單點布置條件下，平板上下表面平均布置各3支熱電偶，在50V電源、2個對稱布置的加熱器條件下，分別測量各點溫度隨時間變化值，并利，用傅里葉導熱定律計算導熱系數，上下表面各點溫差及導熱系數如圖3圖4所示。
 
　　由圖3及圖4可以清晰地看出，多支單點布置熱電偶條件下，各點溫度場隨時間變化的差異是很大的，這樣計算出的導熱系數也有較大的誤差。所以在.這樣的實驗條件下得出的導熱系數具有很大的不可靠性，需要改進實驗條件或實驗方法來準確測量。
 
　　將以上并聯測量不均勻溫度場理論和實驗結果應用到準穩態法測物體熱物性實驗，同樣，保證與上述單點條件下初始條件相同:實驗所需要的電源相同，所測平板及平板上熱電偶布置的位置不變。
平板上下表面平均布置各3支熱電偶，得到上下表面的溫差隨時間變化的關系，如圖5所示。
 
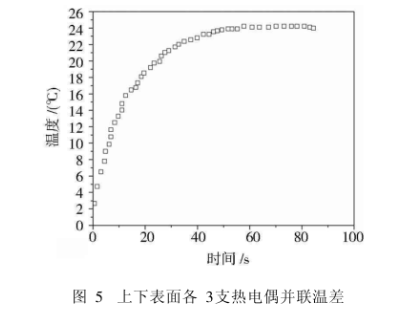
　　忽略通過平板側面即垂直于厚度方向的熱量損失，假設平板熱流密度是按厚度方向傳遞的，利用傅里葉導熱定律，計算導熱系數,測得平板厚度為0.015m，功率為25W，單側熱流密度為12.5W,測得平板導熱系數如圖6所示。
 
　　測量數據顯示，隨時間變化導熱系數趨近于一個穩定值，即驗證了并聯熱電偶在不均勻溫度場條件下能夠準確計算出平板的導熱系數。實驗室里準穩態測熱物性實驗只是在平板上下表面的中心各布置了一支熱電偶，由圖1可以看出，平板表面各點溫度的不均勻性隨時間增加而增大，所以計算出的導熱系數誤差較大;采用并聯熱電偶來做實驗，則可以得到較為準確的實驗結果，而且也解決了由于增加了熱電偶而占據通道數的矛盾,大大提高了實驗的可靠性。
5結論
(1)基于PCL-818HG的溫度采集系統應用廣泛。編寫的程序可以采集不同范圍的電壓信號，不僅可以通過熱電偶溫度傳感器來測量溫度信號，還可以在不同傳感器下測量諸如壓力、密度、高度、位置等信號。
(2)主要針對不均勻溫度場，通過熱電偶的并聯方式來獲得該溫度場的平均溫度。在此基礎上，確定該材料的導熱系數，進而進行各種熱.工計算和實驗研究。
(3)測得的數據及擬合出的并聯值與單點平均值的線性關系，對于直徑為1mm左右的銅-康銅熱電偶有普遍的適用性。