擴散硅壓力變送器的曲面擬合補償

摘要:為解決擴散硅壓力變送器因非線性特性及易受溫度影響從而導致其測量精度降低這一-問題,提出了基于最小二乘曲面擬合的補償方案。建立了傳感器的被測壓力、工作溫度和輸出電壓間的曲面擬合數學模型,在獲得傳感器的輸出電壓和T.作溫度后能簡便地計算出被測點的壓力值。實驗表明,該算法具有較高的補償精度。由于所建擬合模型階次較低，因此補償計算所需時間短,保證了補償算法的可行性。
與其它壓力傳感器相比,擴散硅壓力傳感器具有動態響應快、靈敏度高、體積小、耐振、耐沖擊、耐腐蝕和抗干擾能力強等許多優點，它的主要缺點是受溫度影響較大，輸出具有非線性特性,從而降低了測量精度,為此必須進行非線性校正和溫度補償”。目前采用的補償方法有插值法、曲線擬合法及神經網絡法等。插值法速度快,精度高,但需要預先輸人數據對照表，數據量大，容易出錯。曲線.擬合法和神經網絡法的補償精度較高,但曲線擬合法是通過選擇較高的階數才獲得滿意的精度,公式多,計算量大,響應速度慢,神經網絡法需要的數據量大且編程復雜,一-般的微控制器難以勝任。
　　以傳感器的輸人壓力、工作溫度和輸出電壓為變量,通過最小二乘法以獲得傳感器的曲面擬合數學模型,在測得傳感器的輸出電壓和工作溫度后能快速簡便地計算出被測點的壓力值,取得.了很好的效果。
1最小二乘法原理簡介
　　最小二乘法是用于參數估計的一種數學方法，它使數學模型在誤差平方和最小的意義上擬合實驗數據。。假定有一個變量y,它與一個n維變量X=(x1,x2..,xn)是線性關系,即
y=θx1+θ2x2+...+θnxn
　　其中θ=(θ1,θ2,.,0n)是一個參數集,它們是未知的,希望通過不同時刻y及X的觀測值來估計出它們的值。假設在t1,t2,.,tm時刻對y及X的觀測值序列已經被獲得,并且用y(i)及x1(i),x2(i),x3(i),.,xn(i),(i=1,2,.,m)來表示這些觀測數據。顯然,可以用方程組來表示它們之間的關系
 
2曲面擬合模型的建立
　　對應不同的工作溫度,擴散硅壓力傳感器具有不同的輸人(壓力p)輸出(電壓u)特性。如果能夠確定不同工作溫度t時的u-p特性,那么根據電壓u按反非線性特性求取被測壓力p,從原理上講不存在溫度引入的誤差(2),但在有限數量的幾個溫度值下確定的u-p特性,無法確定任意溫度下的u--p特性.為解決這一問題,引人最小二乘法,在擴散硅壓力傳感器的整個工作溫度范圍內標定u--(p,t)特性,即建立擴散硅壓力傳感器的曲面擬合數學模型,從而可在任意溫度下根據傳感器的輸出電壓u和工作溫度i求得被測壓力p。
　　事實上,擴散硅壓力傳感器的輸出電壓u是被測壓力p和工作溫度t的函數:
u=ƒ(p,t)(3)
　　此處提出以二元多項式來擬合該函數ƒ(p,t),以期獲得輸出u的數學表達式。
　　設u的表達式中,p的最高階次為(m-1),1的最高階次為(n-1),且p和t之間存在耦合關系,則ƒ(p,t)具有如下形式:
 
　　為了得到式(6),需要對傳感器進行標定實驗,檢測有關標定參數(p,t,u),并根據標定參數求得系數矩陣C。標定實驗時,按傳感器的量程均勻選取M個壓力點P1,P2,...,PM,按工作溫度范圍均勻選取N個溫度點t1,t2,...,tN采用標準的溫度控制實驗箱和壓力標定器進行標定實驗,得到MxN組數據(pi,tj,uij)(其中i=1,2,,Mj=1,2,.,N),將MxN組標定數據代人方程(7)，根據最小二乘法原理,得到最小乘解方程如下:
 
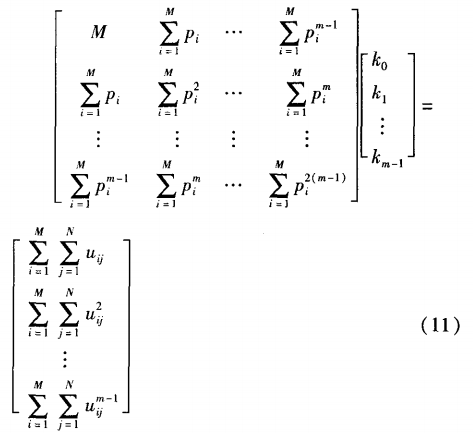
應用最小二乘解，可求出第一次的補償系數k0,k1,.,kmm-1。
　　根據所求的補償系數ho及標定的N個溫度點T1,t2,..,tN,根據方程(8)利用最小二乘原理可求取補償系數c11,c12,.....,cino同理根據方程9)...(10)可求取補償系數C21,2,",Cmn,也即求出了系數矩陣C,從而得到了傳感器的被測壓力、工作溫度和輸出電壓間的曲面擬合數學模型。在獲得傳感器的輸出電壓和工作溫度后,利用該模型便能計算出被測點的壓力值。為方便壓力的計算,提高計算速度,在保證補償精度的前提下,應使曲面擬合數學模型的階次最低,也即使(mxn)最小。
 
綜合考慮計算的復雜度和精度的要求,實際操作步驟如下:
①設定m=2,n=2。
②進行第--次補償,求取補償系數k0,k1.,..,km-1。
③進行第二次補償,求取系數矩陣C。
④將系數矩陣C代人到式(6),得到曲面擬合方程。
⑤用得到的曲面擬合方程計算壓力值,進行精度檢驗。如果精度達不到預定要求,先m=m+1,回到第②步重新進行補償,若仍達不到精度要求,則n=n+1,回到第②步重新進行補償。直到精度達到預定要求則結束。
在求得曲面擬合方程后,在線測量時,根據測得的傳感器的輸出電壓u和工作溫度t,通過曲面擬合函數的反線性特性,可求得被測壓力p。
3補償效果分析
　　選用硅壓力傳感器作為檢測元件,其測量范圍為2~142kPa,工作溫度為(-40~+80)℃，輸出范圍為30~120mV,經過補償后,要求傳感器的精度等級達到0.2%。為了確定補償系數矩陣C,從2~142kPa內選取了8個壓力測試點,從(-40~+80)℃內選取了7個溫度測試點。在每個壓力、溫度點采用標準的溫度控制實驗箱和壓力標定器進行標定實驗,測量其輸出電壓(16位AD值),每個點測量3次,取其平均值作為標定數據,結果如表1所示。
 
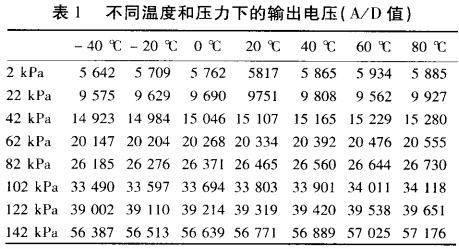
　　根據表1給定的標定數據，按照前述步驟,運用MATLAB編程進行補償分析,求出系數矩陣C,將系.數矩陣C代入方程(6)即得到曲面擬合方程。在進行精度檢驗時,為了更好地檢驗補償效果,所選擇的溫度和壓力值與標定點不完全相同,這樣可以檢驗.非標定點的補償效果,表2.3、4分別為m、n取不同值時的補償結果(m≠n時的數據略)。
 
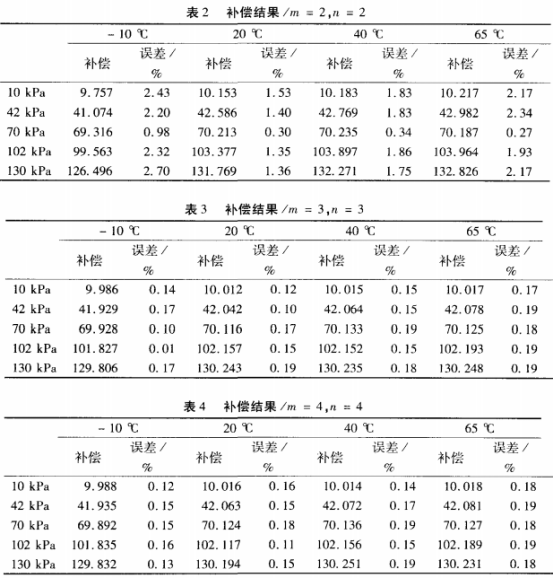
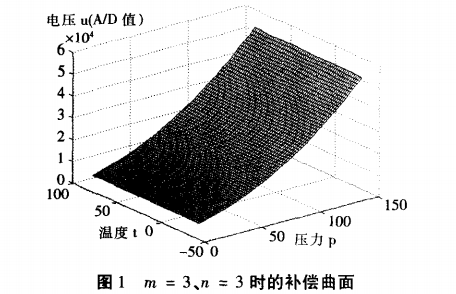
　　從表2、3.4可以看出當m=2、n=2時,補償結果不能達到0.2%的精度等級要求,而m=3、n=3和m=4、n=4時的補償結果均能達到0.2%的精度等級要求。考慮到m=3、n=3時，根據曲面擬合方程(6),由u、t求取p僅需求解一元二次方程,方程具有正確的解析解,且求解簡單快速,而m=4、n=4時方程(6)是--元三次方程,求解不方便。因此實際中采用了m=3、n=3進行補償,此時的補償曲面見圖1所示。
 
4結論
　　擴散硅壓力傳感器的輸人輸出具有非線性特性,且受溫度的影響較大,降低了其測量精度,針對這一問題，提出了最小二乘曲面擬合的補償方案,根據實驗標定數據,運用最小二乘法,建立了壓力、溫度和輸出電壓之間的曲面擬合補償模型。實驗表明,運用該模型進行補償可以將擴散硅壓力傳感器的精度控制在0.2%以內，由于補償模型階次低,使得補償計算非常簡單。.