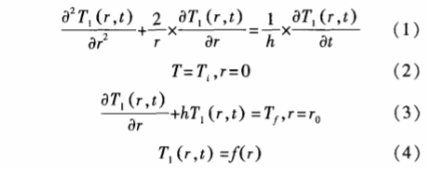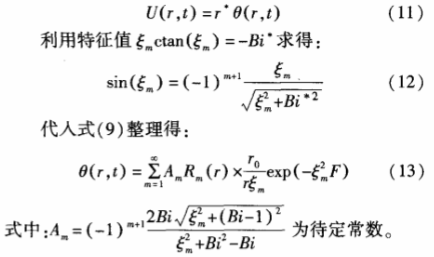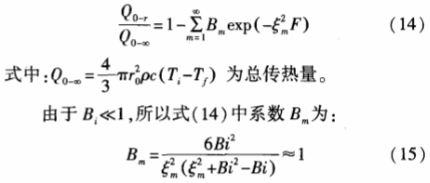一種錫膜熱電偶的動態響應模型

摘要:為了提高銅-康銅錫膜熱電偶溫度傳感器的測量精度以及靈敏性,選取銅~康錒錫膜熱電偶進行--維非穩態傳熱分析。基于牛頓冷卻定理以及傅里葉導熱定律，建立了銅-康銅錫膜熱電偶的動態熱響應模型,對其邊界條件進行綜合比較,對模型進行求解并基于Simulink/Matlab進行動態仿真。通過試驗驗證了動態熱響應模型精度。仿真預測模型簡單,能夠較為正確地模擬銅=康銅錫膜熱電偶的熱響應特性。
0引言
　　熱電偶是根據溫度的變化而產生響應的電熱勢,進而在計算機上顯示出溫度值，因此熱電偶在測溫中不會因自發熱而影響測量精度,在實際應用中表現出優良的性能。但是熱電偶的熱惰性會使得其測溫的實時性受到影響",目前基于熱電偶內部的導熱特性對響應時間影響的報道并不多見。熱電偶時間常數的測試系統，給出了不同范圍溫度、時間常數各異的熱電偶測試曲線，并且通過試驗驗證了此系統的測試精度,可以測試到亞毫秒至秒量級的時間常數。通過對熱電偶導熱特性的分析,建立了熱電偶在管式爐內測溫時的溫度響應模型，得到了熱電偶的溫度響應時間,并且試驗驗證了其理論。基于熱電偶的傳遞函數求得的補償算法可以在單片機內實現對實際溫度的實時采集。從傳感器的結構出發，論述了傳感器的結構、動態和靜態標定,在實際應用中取得了良好的效果。
　　近年來,對薄膜熱電偶的研究越來越多[8],主要是對熱電偶形狀改進的研究。對熱電偶的形狀進行改進,能提高其動態響應時間。但是對于熱電偶動態響應時間的理論模型的研究鮮見報道。
1建立模型
1.1建模理論
　　采用錫膜焊接的方法制作的銅-康銅熱電偶,在錫膜焊接過程中對錫膜直徑控制的精度不高。文獻[9]提出的熱電偶錫膜直徑可控制在0.03~0.5mm,因此在這個直徑范圍內對其進行導熱分析。銅_康銅熱電偶內部結構如圖1所示。
 
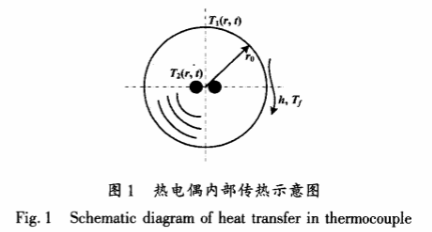
　　圖1中,r0為熱電偶錫膜半徑,h為熱電偶錫膜外表面與熱流空氣的換熱系數。
　　銅-康銅熱電偶在固體表面進行測溫時要保證其密封性,因此可認為測溫過程是熱電偶對其周圍的熱流空氣進行測溫。熱流空氣的溫度通過錫膜傳到熱電偶內部的感應端,錫膜外壁到感應端的溫度從T1(r,t)降低到T2(r,t)。建模思想基于如下假設。
①在熱電偶外表面流動空氣的熱流密度恒定,可忽略接觸熱阻。
②錫膜較薄,可假設溫度為一維球體導熱。
③由于錫膜直徑較小,可認定感應端的兩個球體
與錫膜同心，即熱電偶錫膜外表面到感應端的傳熱距離為r0。
1.2動態建模
　　根據圖1所示熱電偶內部結構,將熱電偶放置在初始溫度為Tƒ的實際工況中,得到一維導熱模型:
 
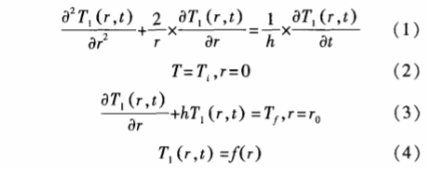
　　式中:h為熱電偶錫膜外表面換熱系數;r為瞬時傳熱距離;r0為錫膜半徑;Tƒ為被測熱流空氣溫度;Ti為熱電偶處于室溫下的初始溫度。
　　引用新的因變量U(r,t)=rT1(r,t),式(1)~式(4)可變換為:
 
 
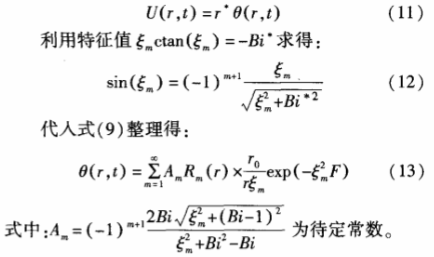
　　綜上可得到錫膜經過t時間的積累瞬時傳熱量Qo-f,將其無量綱化得到:
 
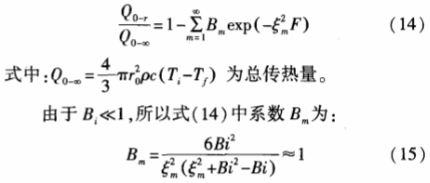
　　熱流空氣與熱電偶錫膜外表面的換熱量表面的對流換熱量可由傅里葉定律得到:.
 
　　式(18)表明，錫膜熱電偶動態響應時間與錫膜直徑r0、導熱系數λ、錫膜外表面換熱系數h以及空氣的熱擴散率α有關。如當錫膜直徑r0增大時,動態響應時間也隨之增大等。
　　綜上所述,式(13)和式(18)為非線性方程,不容易獲得正確解,可基于擁有強大計算功能的Simulink/Matlab,對所述非線性方程組求得熱電偶對熱流空氣進行測溫時的瞬態溫度場,并最終求得熱電偶錫膜直徑對動態響應時間常數的影響。
2數值仿真
　　在Simulink下對表1中的初始工況進行仿真,得到3種直徑下的熱電偶的動態響應情況如圖2所示。
 
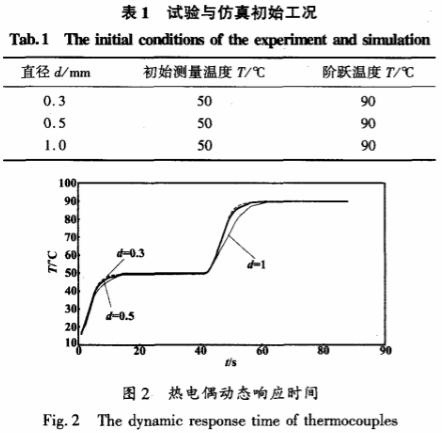
　　圖2表明,熱電偶隨著其錫膜直徑的增大,其動態響應時間增加,尤其是當錫膜直徑為1mm時,熱電偶的滯后性明顯,可見熱電偶的動態響應時間取決于錫膜直徑，直徑越小，動態響應時間越短。
　　基于Simulink動態仿真模型得到熱電偶錫膜直徑對時間常數的影響如圖3所示。
 
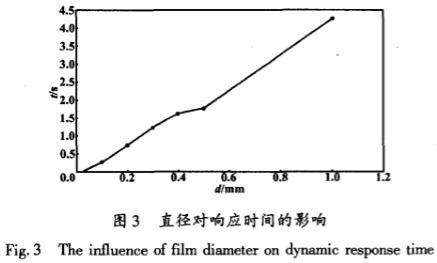
　　圖3表明，熱電偶的動態響應時間常數t隨著錫膜直徑的增大呈線性增大的趨勢。當錫膜直徑為1mm時,動態響應時間突然增大，不能滿足實際測溫要求。因此,要求對熱電偶錫膜的直徑進行嚴格的控制。由仿真結果可知,當錫膜直徑在0.03~0.3mm范圍內時,熱電偶的動態響應時間常數較小，因此應盡量控制在此范圍內,以便正確測溫。
3試驗驗證
　　為了進一步對熱電偶的動態響應時間進行描述,取錫膜直徑為0.3mm的熱電偶進行標定[10]以及試驗驗證,采用安捷倫萬用表自動采集溫度,采用測溫精度更高、響應時間更短的A級Pt100溫度傳感器對熱電偶進行驗證。試驗中,將A級Pt100溫度傳感器的溫度作為實際溫度,并將熱電偶測量到的試驗值與仿真值進行對比分析。試驗示意簡圖如圖4所示。
 
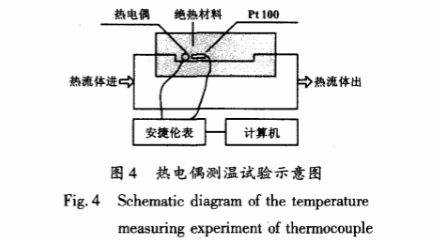
　　將A級Pt100溫度傳感器、熱電偶分別放置在溫度為50℃的被測熱流空氣中,要求Pt100溫度傳感器放置在熱電偶附近。當熱電偶測量值趨于穩定時,逐.漸提高被測熱流空氣溫度直到90℃并在90℃保持恒溫。試驗值與仿真值對比如圖5所示。
 
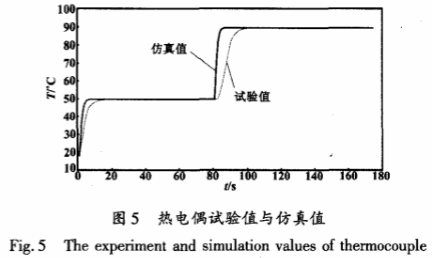
　　由圖5可以看出:①在20~50℃階段,熱電偶的試驗值略低于仿真值;②在50℃的準穩態階段，試驗值略大于仿真值,表明模型在準穩態階段對于熱電偶實際工況能夠進行較為正確的仿真模擬;③在50℃.上升到90℃的階段，試驗值表現出明顯的滯后，說明模型的邊界條件不能非常正確地描述熱電偶的實際測溫特性,同時試驗值與仿真值之間的誤差也是由于對熱流空氣的溫度加熱并不能實時與理想仿真中的溫度上升值相匹配;④在90℃的準穩態階段,試驗值與仿真值符合得較好。
　　為了更加直觀地說明模型的仿真值與試驗值之間的關系,對試驗值與仿真值求絕對誤差,如圖6所示。
 
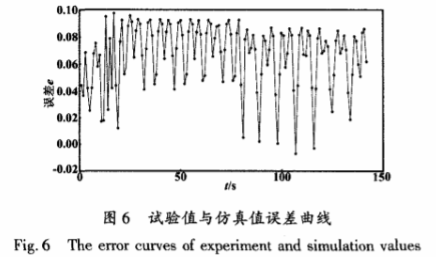
　　圖6所示曲線表明,在采用熱電偶進行測溫時，記錄數據要有一定的延遲，并且熱電偶在準穩態階段測溫時的誤差精度基本為10^-2。綜上所述,要求熱電偶盡量在準穩態階段進行數據的采集。錫膜熱電偶不適合在溫度階躍變化頻率較大的工況下使用。如果溫度在產生階躍以后維持10s左右，則對錫膜熱電偶采集到的溫度值求平均溫度后,其測量精度還是較為正確的。
4結束語
　　對熱電偶在測量熱流空氣時進行動態建模,模擬出熱電偶測溫的動態特性，并且得到熱電偶錫膜直徑對其動態響應的影響,對熱電偶制作以及測溫具有指導意義。試驗驗證了動態響應模型具有較高的精度，錫膜熱電偶在測溫過程中具有滯后性,熱電偶適用于準穩態工況以及溫度階躍頻率較低的測溫工況,不適合溫度變化較大且階躍頻率較高的工況。仿真模型簡單,能較為正確地描述錫膜熱電偶的動態測溫特性,可適用于其他溫度傳感器的動態響應仿真模擬。