Ｅ型熱電偶動態(tài)特性研究

摘要：以Ｅ型熱電偶為研究對象，采用溫度采集模塊、通過VisialBasic和DCONUtility軟件實現(xiàn)了實驗數據的自動采集，完成了Ｅ型熱電偶的動態(tài)特性實驗，并使用MATLAB對實驗數據進行了可視化研究，得出了該類型熱電偶在不同偶絲直徑、不同插入深度以及不同被測溫度下的數學模型，為該類型熱電偶在火電廠安裝、檢修時提供必要的理論基礎與實踐指導。
1引言
       在火力發(fā)電廠中，雖然各類型溫度傳感器都有相應的安裝規(guī)范與技術要求，但在施工過程中，由于施工人員的不能嚴格按照要求進行安裝調試，經常會出現(xiàn)溫度傳感器損壞、測量回路異常、溫度信號的閾值設置不合理等現(xiàn)象的發(fā)生，而這些故障或者事故的發(fā)生，往往會造成溫度信號突變引起保護對象的誤跳閘，進而引起保護誤動作或拒動，造成機組的非計劃減出力或停運，給電力系統(tǒng)帶來巨大損失。由于上述問題的嚴重性，國內外不少技術人員和專家都對該類問題進行過相關的研究與分析，做過諸如對溫度傳感器進行靜態(tài)特性測試［1－2］的研究與分析、校驗設計與測量數據處理［3－4］的討論、同時也有對熱電偶的動態(tài)特性［5－6］進行實驗設計與研究、還有對該類問題進行過數學建模分析［7］。本文以Ｅ型熱電偶為例，設計一套完整的動態(tài)實驗系統(tǒng)，得出Ｅ型熱電偶測溫時，相對誤差（精度）與插入深度、時間常數以及偶絲直徑之間的關系，并且建立了對應的數學模型，為該類型熱電偶在火電廠安裝、檢修、維護時提供必要的理論依據與實踐指導。
2實驗設計
2．1實驗設備
如表1所示。

2．2實驗系統(tǒng)
       如圖1所示，設計該實驗系統(tǒng)。

       該實驗系統(tǒng)包括校驗儀（作為標準熱源）、Ｅ型熱電偶、熱電偶信號采集模塊、轉換模塊、電源和工控機，工控機通過RＳ－232串口與轉換模塊Ｉ－7520、采集模塊Ｉ－7018、校驗儀相連，由于熱電偶的使用溫度受材料規(guī)格和直徑的影響，因此，Ｋ型熱電偶的長度為15cm，直徑為2～5mm，電源為DR－75－24開關電源，范圍為10Ｖ～30Ｖ，電源供應器的額定功率大于整個系統(tǒng)的消耗功率的總和。
2．3實驗步驟
1）開啟電源，啟動干式爐升溫；運行應用程序，設定被測溫度和采集時間，選擇接收端口和采集周期；當干式爐升溫至設定溫度并穩(wěn)定時，將熱電偶快速（形成類似于階躍信號的輸入）插入干式爐中，同時點擊工控機界面上的“開始采集”按鈕，實驗開始；
2）在實驗過程中，保持熱電偶固定，直到響應曲線平穩(wěn)，點擊工控機界面上的“停止采集”按鈕，將熱電偶取出，點擊工控機界面上的“保存數據”按鈕，保存實驗數據和圖像；
3）當熱電偶冷卻至室溫后，分別改變熱電偶插入干式爐中的深度、干式爐的設定溫度和熱電偶的直徑，重復步驟1）和步驟2），獲得熱電偶的插入深度、溫度和直徑的階躍響應曲線，建立在不同熱電偶直徑條件下，相對誤差與插入深度和溫度之間的數學關系式、時間常數與插入深度和溫度之間的數學關系式；從而很直觀的看出熱電偶插入深度、直徑對熱電偶測溫性能的影響，對火力發(fā)電廠中不同的測溫部位選擇合理的熱電偶溫度傳感器，以實現(xiàn)溫度滯后的最小化有著一定的指導性作用。
2．4動態(tài)特性響應曲線
       根據上述實驗步驟，分別做了直徑¢＝2mm、¢＝3mm、¢＝4mm、¢＝5mm，溫度點從室溫分別到100℃、200℃、300℃、400℃時，插入深度與所測溫度之間的階躍響應曲線。
下面取一組實驗數據，當溫度為300℃時，熱電偶的偶絲直徑、插入深度與被測溫度之間的階躍響應曲線，如圖2（ａ－d）所示。
從上述四組圖像中可以看出：
1）階躍響應曲線趨勢一致；
2）熱電偶的偶絲直徑為過小時（¢＝2mm），熱電偶的階躍曲線容易出現(xiàn)波動，誤差比較大；
3）當¢＝4mm、5mm時，插入深度為2cm已經不符合其安裝規(guī)范，其響應曲線異于正常曲線，所測數據為錯誤數據；
4）時間常數隨著溫度階躍變化量的增大，先呈現(xiàn)上升趨勢，而后下降。
本次實驗工作，完成了偶絲直徑¢＝2mm、¢＝3mm、¢＝4mm、¢＝5mm，溫度點從100℃、200℃、300℃、400℃的階躍實驗，所有這些實驗數據趨勢一致，與上面圖例類似，由于篇幅所限，本文只選擇其中一組進行分析與說明。

3數學建模
       通過接口程序，將Excel表中的幾千組實驗數據以數組方式讀入MATLAB軟件中，利用ＭＡＴ－ＬＡB強大的數據可視化功能進行擬合，得出下列公式。
3．1精度與被測溫度及插入深度的關系
       基于上述動態(tài)實驗測試方案，對相對誤差（精度）與被測溫度以及插入深度進行了數學建模，如表2所示。

       其中，ｃN—¢＝N（mm）時，Ｅ型熱電偶測量時的相對誤差；bN—¢＝N（mm）時，被測溫度；dN—¢＝N（mm）時，Ｅ型熱電偶的插入深度；N＝2，3，4，5。
通過Matlab軟件進行了可視化研究，如圖3（ａ－d）所示。

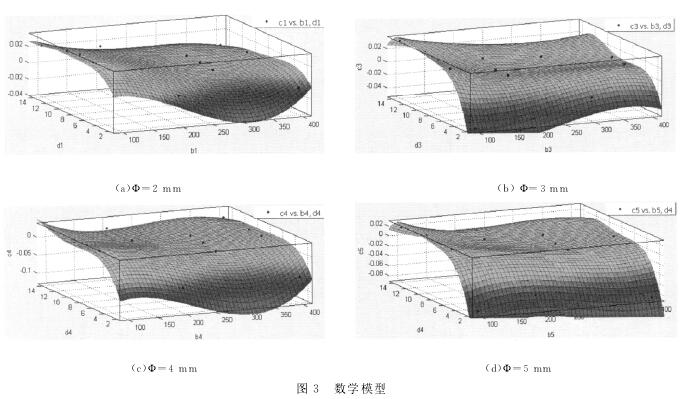
4．2時間常數與被測溫度及插入深度的關系
       熱電偶的時間常數［8－９］也歷來是一個研究重點，本文基于上述動態(tài)實驗測試方案，對時間常數與被測溫度以及插入深度進行了數學建模如下表3所示。

       其中，ｅN———¢＝N（mm）時，Ｋ型熱電偶的時間常數；bN———¢＝N（mm）時，被測溫度；dN———¢＝N（mm）時，Ｋ型熱電偶的插入深度通過Matlab軟件進行了可視化研究，如圖4（ａ－d）所示

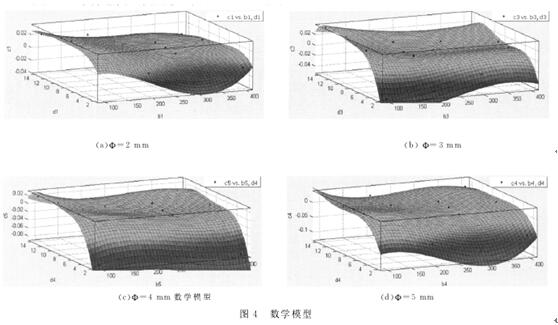
4．3驗證
      為了驗證表2和表3所示的數學模型的正確性，取一支¢＝4mm的Ｋ型熱電偶作為待測熱電偶進行實驗，測量溫度分別為100℃、200℃、300℃、400℃，插入深度分別為2cm、6cm、8cm、10cm、14cm進行了數據采集如表4所示。
  
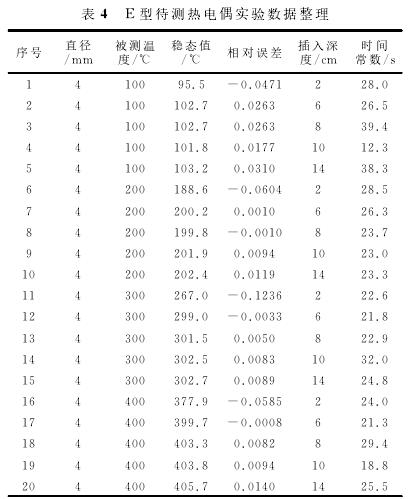
       將上述數據帶入上述相應數學表達式，計算Ｅ型待測熱電偶的精度，符合其精度要求，說明上述數學模型可以方便快捷地驗證所選熱電偶精度、粗細、安裝等是否合理，為電力生產過程中的Ｅ型熱電偶的選型、安裝提供了一定的理論與實驗依據。
5結論
       綜上，本文以Ｅ型熱電偶為研究對象，對直徑為¢＝2mm、¢＝3mm、¢＝4mm、¢＝5mm的熱電偶通過階躍響應實驗完成了數學模型的可視化研究，并驗證了該數學模型的正確性，得出以下四點結論：
1）插入深度對測量誤差的影響尤為明顯，對于本文所用Ｅ型熱電偶，其插入深度要求為直徑的15～20倍，而文中熱電偶插入深度為2cm時，不符合安裝規(guī)范，其相對誤差也較大。
2）插入深度與相對誤差并不成線性關系，而是相對誤差隨著插入深度先減小，后增大。
3）在允許測量范圍內，熱電偶測量的相對誤差隨著被測溫度的升高而降低。
4）熱電偶直徑越小，顯示溫度越容易出現(xiàn)波動，越容易產生誤差，對于系統(tǒng)穩(wěn)定是不利的。
5）熱電偶直徑越小，時間常數越小；該熱電偶的時間常數隨溫度階躍變化量的增大，先呈上升趨勢，而后又有所下降，隨后呈現(xiàn)較大幅回升，預測變化趨勢為隨溫度階躍變化量逐漸升高。