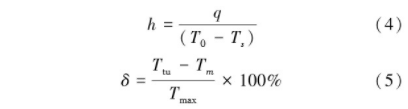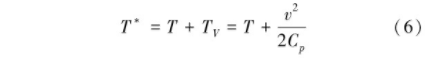分度熱電偶時參考端溫度對測量結果的影響
發布時間:2022-10-08
瀏覽次數:
摘要:為分析涂層測溫結構對航空發動機渦輪導向葉片表面溫度測量精度的影響,建立了測溫結構的數學模型。以熱流耦合理論為基礎,采用SST-γ-θ湍流模型求解動量和能量方程,研究了涂層位置、涂層厚度和前緣形狀對葉片待測區城溫度的影響。研究表明:考慮轉捩的SST-γ-θ具有較好的數值計算精度,其溫度計算結果與試驗誤差不超過10%;當涂層前緣位于轉捩點附近時,涂層對測量精度的影響較大;與葉盆中部和葉背前緣相比,涂層對葉背中部和葉背尾緣的測溫精度影響較小;當涂層厚度小于總溫邊界層厚度時,測量精度幾乎不受影響;將涂層前緣加工成圓角可以有效減小涂層對葉盆面測溫精度的影響。
航空發動機作為航空飛行器的動力裝置,正不斷向大推力、大推重比的方向發展。隨著航空發動機性能的提高,其工作溫度也相應地持續提高。20世紀60年代以來鎳基單晶合金材料的耐高溫性在渦輪葉片制造中提高了102℃。近年來,發動機工作溫度接近甚至超過材料的許用溫度,熱端部件表面溫度的準確測量對發動機設計水平的提高具有重要的現實意義。
目前,渦輪導向葉片表面溫度主要的測量方法有傳統
熱電偶測溫、紅外輻射測溫[3]、示溫漆測溫、
薄膜熱電偶測溫等。由于熱電偶具有結構簡單.制造方便、測量范圍廣、精度高、慣性小和輸出信號便于傳輸等諸多優點,一直都是航空發動機葉片測溫的主要測量元件。通過熱電偶測量葉片表面溫度的主要難點在于安裝和制備方法。由于葉片表面光滑,傳統使用中熱電偶是通過填埋或金屬蒙皮的方法固定在金屬表面的。采用填埋安裝時,由于葉片厚度方向的溫度梯度,測量點溫度難以與表面保持一致,因而無法準確測量葉片表面溫度,此外還會造成試件表面的破損。而采用金屬蒙皮焊接固定又會導致熱電偶受感部周圍存在縫隙,造成較大的接觸熱阻。為解決傳統熱電偶安裝方法中存在的弊端,提高渦輪葉片表面溫度測量的精度,一種將熔融態耐高溫絕緣材料Al2O3粉末直接噴涂至渦輪葉片基底上的熱電偶安裝方案,簡稱為涂層測溫。該方案的工藝流程為:①表面吹沙處理,增加待測表面粗糙度;②使用高能等離子噴槍噴涂Al2O3粉末,材料,形成絕緣層;③利用高溫膠帶和等離子材料噴涂工藝完成功能層制備;④利用高溫膠帶和Al2O3粉末制備保護層;⑤通過平行微隙焊接工藝和激光焊接技術完成熱電偶裸絲與后端高溫補償導線連接,最后將高溫膠帶揭去,完成涂層制作。
相對于金屬蒙皮Al203涂層、金屬基底和熱電偶頭部之間幾乎不存在接觸間隙,是一種新式的熱電偶安裝制備工藝。但涂層具有一定的厚度,其邊緣易對渦輪葉片表面的燃氣流動產生干擾,該測量方法的準確性還有待進一步的評估和驗證。
由于實際渦輪葉片測溫試驗中,影響涂層測溫精度的因素較多,如固體導熱接觸熱阻、輻射環境、信號傳輸及處理等,難以通過試驗手段精確分析某單一因素對誤差的影響,且多次試驗成本較高。近年來,隨著CFD熱流耦合技術的發展,對流體換熱問題的計算精度有較大提高,較多研究者開始采用仿真方法預測渦輪葉片的工作環境和表面溫度。
為詳細分析涂層測溫中涂層對葉片表面溫度和燃氣環境的影響,以MarkI葉片為原型,根據實際情況,建立4個典型位置的涂層模型,基于熱流耦合仿真技術,討論涂層的位置、厚度和前緣形狀對渦輪導向葉片表面溫度的影響,為提高葉片表面溫度測:量準確性,修正熱電偶測量誤差提供參考。
1物理模型及計算方法
1.1計算模型
所研究的葉片葉型數據參考文獻[16]的葉片平面坐標和高度數據,通過Workbench-DM建模軟件中的樣條線(curve)擬合而成,然后經放樣計算獲得整個葉片的三維模型。該葉片為MarkII型導向葉片,其幾何參數如表1所示。
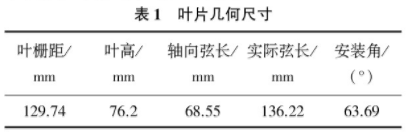
典型的熱電偶涂層安裝試件如圖1所示。根據.熱電偶涂層的結構,在MarkI葉片模型上,建立了4個涂層的典型位置,分別位于葉背前緣、葉背中、葉背后緣、葉盆處,標準的涂層尺寸為50mmx50mmx1mm。葉片模型及涂層的位置如圖2所示。其中,圖2a)中2處黑線位于涂層下方葉片表面50%葉高處,表示實際使用中熱電偶測量點可能處于的位置,命名為A線和B線。考慮到涂層多采用噴涂形式,邊緣一般會帶有一定的圓角,為研究圓角半徑R對測量點附近溫度的影響,在1mm厚度涂層模型的基礎上建立了3種圓角形式,如圖2b)所示。


選用5411號試驗工況,其進出口邊界條件如表2所示。葉片中有10個徑向圓柱形對流冷卻孔,其直徑,冷卻氣體質量流量、中徑處平均總溫Tmid和冷卻氣體進口總溫Tin見表3,冷卻氣體出口靜壓為175713Pa。

1.2材料參數
數值計算中,流體的工質設為理想可壓燃氣,其定壓比熱容Cp為1004.4J/kg·K,分子黏性μ和導熱系數K均表示為溫度T的函數

涂層的材料為氧化鋁(純度為96%),其密度為3800kg/m³,導熱系數為25W/m·K,比熱容為880J/kg.K。
1.3網格劃分
對湍流的模擬選用Menter和Langtry提出的間歇因子與動量厚度的雷諾數雙方程SST-γ-θ湍流模型[2]。該轉捩模型是基于局部變量的轉捩模型,并對前人提出的模型作了較大改進,通用性和準確性都得到很大提高[23]。網格采用ANSYS-Workbench提供的Mesh工具進行劃分。由于邊界層內流體的速度和溫度變化較大,需要對邊界層內網格進行加密。根據進出口條件估算葉片附近氣體的雷諾數為10量級,為滿足SST-γ-θ模型計算精度要求,需要y*數盡可能接近于1。根據CFD-Online提供的y'計算器的估算結果[24],將近壁面第一層網格厚度劃分為1μm,此后每層間距以1.5的比率增加,共劃分了15層近璧面網格。在葉片冷卻通道內以同樣方法生成近壁面網格,其第一層網格厚度為0.01mm,增長比為1.5,共15層。燃氣區采用混合網格劃分,葉片和涂層部分則采用以六面體為主導的網格劃分。涂層部分在涂層厚度方向上劃分為10層網格,在流-固、固-固交界面網格進行加密。網格交界面數據采用generalgridinterface(GGI)格式傳遞。經網格獨立性試驗選擇網格總數約為908萬。其中,流體網格為775萬、葉片網格為70萬、涂層網格為64萬,網格如圖3所示。

1.4求解過程
邊界設置為無滑移壁面,燃氣兩側采用周期性邊界條件。傳熱模型為總能模型,求解格式為二階向后歐拉法,湍流數值采用精度高求解格式。當氣體馬赫數達到0.3以上時,氣體動能對換熱的影響變得顯著,因此設定傳熱模型為總能模型,并使用CFX特有的高速壁面換熱模型增加求解精度。當連續性、動量、湍流和能量各殘差曲線和設定的監測點溫度趨于穩定,所有的流體進出口質量流量相對誤差小于10
-6時,認為計算收斂。為方便對比定義對流換熱系數h、相對溫差δ為
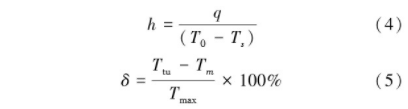
式中,T0為燃氣入口總溫,Ts表示固體溫度,Ttu為tu帶有涂層時的葉片溫度Tm為無涂層葉片表面溫度,max為無涂層葉片最大溫度,根據仿真結果,其值取為688K。
2結果及討論
2.1計算結果驗證
數值策略的驗證采用了Hylton[17]報告中5411號試驗的結果數據。分別取無涂層及涂層厚度為1mm時,50%葉高處的壓力、對流換熱系數及溫度結果與試驗值對比,對比結果如圖4至6所示。由圖4可見,無涂層葉片壓力計算結果和實驗數據吻合較好,在吸力面上軸向弦長(軸向弦長記為L)約X/L=0.2和X/L=0.4處前后都存在較大的壓力梯度。值得注意的是此處SST-γ-θ模型的預測結果與實驗值有一定的偏差,這是因為激波發生附近邊界層分離誘發轉捩,邊界層內梯度較大,產生所謂“激波-邊界層”相互作用。在燃氣流經激波面時,燃氣中的壓強、密度、溫度和流速都會發生較大的變化,因此激波點可視為間斷點,具有很強的非線性特征,造成較大的計算誤差,這也是目前一個公認的有待解決的數值計算問題。
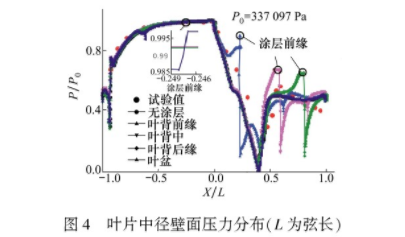
如圖6所示,激波附近葉片表面溫度突然下降后急劇上升,原因是轉捩點附近發生附面層分離,氣體內能向動能轉化,燃氣溫度下降。激波后附面層重新生成,氣體的湍流動能得到加強,換熱速度增加,溫度上升。由圖5和圖6可知,無涂層葉片表面中徑處傳熱系數h和無量綱的靜溫T的分布趨勢與實驗相仿,盡管在吸力面有一定偏差,但多數偏差點小于10%,在可接受范圍內。

2.2涂層位置的影響
涂層在葉片不同位置時的表面流線分布及表面溫度分布如圖7所示。如圖7a)所示,葉片表面的流線在涂層周圍形成繞流,在涂層前后緣形成漩渦。當葉片表面覆蓋涂層時,表面流動狀態與流體流動時遭遇障礙物的情況相似。根據張俊婷等人[28]的研究,當流體流經長方體障礙物時,在障礙物的最高點處即出現邊界層分離,且長方體的回流區比半圓形障礙物和流線型障礙物大。由于涂層的結構近似為長方體,故在涂層的前壁面最高點處也會發生邊界層分離現象,分離點的氣體流速及換熱系數波動較大。如圖4和圖5所示,涂層前緣和尾緣均出現較大的壓力和傳熱系數波動。盡管局部的傳熱系數較大,但相對于整個涂層邊緣處的面積很小,經過涂層的展向傳熱(固體導熱)邊緣處的溫度分布仍比較均勻。如圖7b)所示,涂層邊緣處溫度略微升高,可以推斷實際使用中測量點靠近涂層邊緣時,可能導致測量值偏大。

圖8為涂層位于不同位置時,葉片中徑面的相對溫差分布。由圖中可知,涂層處葉片溫度明顯升.高,當涂層位于葉背前緣時,溫度波動最大,相對溫差達到12.8%。根據圖4至圖6的計算結果,涂層.前緣位于轉捩點附近時,易發生速度邊界層分離造成較大的溫度波動。使用涂層測溫時應避免涂層前緣位于轉捩點附近。同時,可以觀察到涂層的前緣和尾緣處,葉片溫度明顯高于其他位置。

2.3涂層厚度的影響
引入涂層后,葉片表面的燃氣環境所受影響較大,如圖4和圖5所示,涂層前后均出現明顯的波動,除此之外涂層還導致轉捩、回流等現象發生。由于涂層周圍氣體流動的狀態非常復雜,因而單獨討論其對速度邊界層或熱邊界層(即:溫度邊界層)的影響都不足以說明引人涂層后葉片溫度發生改變的原因。葉片與燃氣間熱交換過程的本質是氣體內部分子碰撞金屬表面將動能傳遞給金屬表面分子的過程。在不考慮輻射情況下,氣體和固體間的熱交換的驅動力由兩部分組成,一種為大量氣體分子的宏觀運動,即動溫,Tv;一種為氣體分子的無規則運動,即靜溫,兩者之和為氣體的總溫,其表達式為
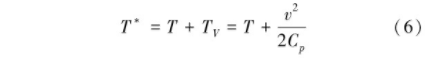
式中,υ為氣體的流速。為分析涂層對葉片對流換熱的影響,定義總溫邊界層的厚度為從物面到約等于99%外部流體總溫處的垂直距離。取涂層前緣周圍6mmx8mm的局部區域為分析對象,其近壁面氣體總溫的分布形式如圖9所示。

總溫邊界層的厚度用于表示單位面積內固體能夠從氣體內獲得能量的大小。工程上希望采用涂層測溫方法后,總溫邊界層厚度可以盡量維持原狀,以確保葉片溫度不受到涂層的影響。因此,在理想情況下涂層厚度應盡可能小于總溫邊界層的厚度。由圖9可知,葉盆面總溫邊界層的厚度低于葉背面,因此,葉盆面的總溫邊界層對涂層的厚度更加敏感。對比葉盆區和葉背區涂層對總溫邊界層的影響可知,在同樣厚度下,葉盆區的總溫邊界層厚度低于葉背區。進一步對比總溫邊界層厚度的相對增加量(總溫邊界層厚度的相對增加量=(添加涂層后的總溫邊界層厚度-無涂層時的總溫邊界層厚度)/無涂層時的總溫邊界層厚度))可知,葉盆區總溫邊界層厚度的相對增加量明顯大于葉背區。這也是葉背區涂層對測溫的影響遠小于葉盆區的主要原因。

圖10為涂層厚度對標記線A、B無量綱溫度的影響,定義C為涂層沿流線方向的長度。如圖10a)所示,葉背處涂層厚度對溫度的影響小于葉盆面,當涂層厚度大于0.5mm時,涂層厚度對葉盆區溫度的影響增加;當涂層厚度大于2mm時,葉背面的溫度才開始受到較大的影響,這進一步說明了總溫附面層厚度與涂層厚度之間的關系。從計算結果分析,僅當涂層厚度小于0.5mm時,熱電偶涂層才不會對涂層測溫的精度造成較大的影響。此時,有涂層時的溫度與無涂層時溫度接近相等,平均相對溫差僅為2%。
2.4涂層圓角的影響
圖11為涂層前緣平面垂直于葉片表面和涂層前緣為圓角時的馬赫數分布圖。當涂層前緣平面與葉片表面垂直時,涂層前緣的平面阻礙了流體的運動。氣體直接撞擊涂層的前緣,形成了很小的氣旋(如圖11中速度矢量圖所示),氣旋消耗了氣體的動能并降低了氣體的流速,因而流過垂直涂層壁面的氣流沒能加速形成激波。當涂層前緣為圓角時,流線型的涂層前緣減小了氣動阻力。在這種情況下氣體的流速進一步增加,在流經涂層前緣后形成了一個弱激波。與葉背前緣的強激波相似,燃氣流經涂層前緣的弱激波后,燃氣的溫度先下降后升高。
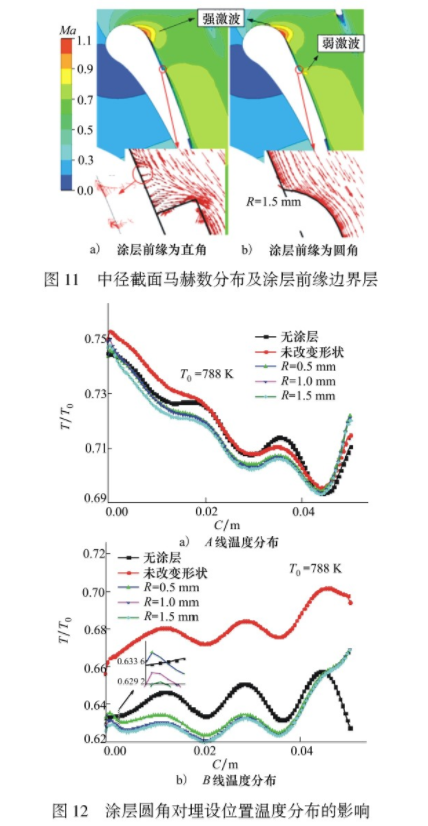
圖12為涂層前端圓角的半徑對標記線A、B無量綱溫度的影響。
如圖12a)所示,當位于葉背中部的涂層前端為圓角時,受到激波的影響,沿燃氣流動方向涂層區的溫度先偏小再增大。如圖12b)所示當位于葉盆區中部的涂層前緣為圓角時,沿燃氣流動方向的溫度.同樣呈現先偏小再偏大的規律,但兩者的作用機理是不同的。當葉盆區的涂層前緣為圓角(流線型)時,涂層前端不會發生激波。此時,涂層對葉盆區測溫的影響僅體現為涂層自身的隔熱作用。由于葉盆面的對流換熱速度較低,涂層起到了明顯的隔熱作用。
3結論
基于熱流耦合技術研究熱電偶安裝涂層對渦輪導向葉片溫度測量精度的影響,分別比較涂層厚度、位置及形狀對常規測量點附近氣動參數及溫度的影響,主要結論如下:
1)葉片表面不同位置的溫度受涂層的影響程度不同,葉背區中部和尾緣的涂層對測溫的影響遠小于葉盆區中部和葉背區前緣的涂層,當涂層前緣靠近葉片轉捩區時,測溫誤差將大幅增加;
2)熱電偶涂層會使總溫邊界層的厚度增加,相比于葉背,葉盆面的總溫邊界層厚度受涂層影響較大,當涂層厚度等于或大于總溫附面層時測量誤差將大幅度.上升,當涂層厚度小于0.5mm時,涂層測溫的精度達到98%;
3)涂層前緣為圓角時可有效避免涂層前緣的燃氣流發生流動滯止,從而提高涂層測溫的精度,與葉背中部相比,涂層前緣形狀對葉盆中部的測溫精度影響更大。