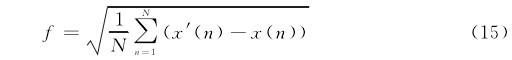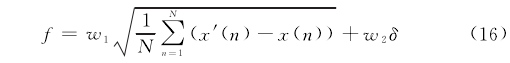基于HHO算法的鎧裝熱電偶動態補償方法

摘要:由于鎧裝熱電偶的時間常數較長、動態特性差,在動態測試中會產生動態誤差,往往不能滿足實際測量需求。提出一種基于哈里斯鷹優化算法(Harrishawkoptimization,HHO)的動態補償模型設計方法,使用該補償模型,改善了鎧裝熱電偶的動態特性。采用基于高溫檢定爐的實驗系統得到鎧裝熱電偶的動態標定實驗數據,同時使用HHO算法優化選取動態補償模型的參數，完成動態補償模型設計。實驗表明:通過此試驗系統及方法可將鎧裝熱電偶的時間常數從37.33s減小到1.91s。在某些特定工作環境下，可使用此方法改善熱電偶傳感器的動態特性,延長其使用壽命,降低成本。
0引言
　　在現代軍工、汽車、化工和火力發電等領域中，能準確獲取快速變化的溫度信息十分重要,這對溫度傳感器的動態特性提出了更高的要求。熱電偶是一種常用的溫度傳感器,擁有成本低、使用簡單等優點,但是受熱慣性等因素影響,在測量瞬態溫度時會產生較大的動態誤差。鎧裝熱電偶在普通熱電偶上增加了金屬套管保護結構,在高溫、高壓、高沖擊與化學腐蝕等惡劣環境下擁有比普通熱電偶更長的使用壽命。但鎧裝熱電偶的保護套管會影響偶結的有效熱交換，使動態誤差進一步增大。在動態測試實驗中,無鎧裝熱電偶與鎧裝熱電偶的時間常數有較大差異所以探索研究鎧裝熱電偶的動態響應特性的改善.方法很有研究及實用價值。
　　改進熱電偶的結構與構建動態補償模型進行補償,是減小動態誤差的兩個常用方法其中,建立動態補償模型具有成本低、效果好、易于實現等優點,已被廣泛應用于多種傳感器領域。本文采用逆模型的思想，即不依賴于傳感器的正向模型,根據輸人輸出數據,通過算法得到補償模型參數進而完成設計[4]常用的參數求解方法有群體智能算法、最小二乘法等,其中群體智能算法可以通過不斷迭代來尋找最優解。
　　并且在很多情況下都能取得較高的收斂速度,且具有易于實現,適應力強,參數設置少,全局搜索能力強等優點0,本文使用群體智能算法來設計補償模型。粒于群算法(particleswarmoptimizationPSO)、遺傳算法(geneticalgorithm,GA)等經典的群體智能優化算法雖然有較快的收斂速度,但存在精度低等缺點。本文選擇的哈里斯鷹優化算法(Harrishawkoptimization,HHO)[6]算法有著收斂速度更快、穩定性強.機理簡單和精度高等諸多優點。
　　在熱電偶動態補償領域,李曉丹等口采用高溫火焰法獲取動態標定數據并采用PSO算法獲取補償逆模型;采用水浴法標定熱電偶并分別通過改進灰狼算法與煙花算法提高了補償逆模型精度;則采用半導體激光器為熱源激勵熱電偶,并采用量于粒于群算法建立補償逆模型。其中,高溫火焰法的火焰溫度難以調整,且溫度存在波動;水浴加熱法的溫度較低，無法反映熱電偶在高溫環境的受熱情況;采用激光器對熱電偶校準的方式則與多數實際應用場景差距較大,適用范圍較窄。熱電偶在水浴、油浴環境中以熱對流為主,本文采用高溫檢定爐為換熱環境，則是以熱輻射為主田,且可以產生精確的恒溫環境,相比于其他動態校準方法能更加的還原各種以熱輻射為主要換熱方式的工業窯爐環境,獲取的數據更貼近此類應用場景。
　　本文選用K型熱電偶,在高溫檢定爐獲取了其鎧裝形式在在高溫環境下的動態響應數據,其次選擇動態補償模型以及階數,隨后利用HHP的全局尋優能力獲取模型的參數完成設計，這種方法對鎧裝熱電偶的動態特性有很大提升。
1基于高溫檢定爐的動態校準方法
　　熱電偶的動態校準需要借助可產生溫度階躍信號的裝置,常用的方法有火焰加熱法”、水浴或油浴快速投擲法[]，激光照射法"”與熱風洞法[1等。熱電偶在不同被測環境下會表現出不同的動態特性,同一支熱電偶在火焰加熱環境與水浴加熱環境中時間常數也有很大差異[*]所以，如果要了解熱電偶在某特定換熱條件下的動態特性并設計補償環節,在相同或相近環境下進行動態標定是必不可少的。本文選擇用高溫檢定爐作為測試環境，目的是更真實的還原熱電偶在高溫熱輻射為主的換熱環境,使獲得的動態補償模型適用于此類動態測試場景。補償模型可應用于陶瓷和石化等行業的生產過程中的溫度動態測量,從而指導產品工藝設計。
　　基于高溫檢定爐的動態校準系統如圖1所示,由高溫檢定爐.傳感器快速給進裝置、調理電路、采集卡以及上位機組成。通過溫度控制器控制爐內加熱繞組,將爐內恒溫區加熱到指定溫度。傳感器快速給進裝置由步進電機控制,可以調節速度以及停留位置。熱電偶通過傳感器快速給進裝置,從爐口快速進人檢定爐恒溫區并停留，如圖2所示。由于爐口到恒溫區距離為12cm,溫度大致呈線性上升,傳感器快速給進裝置的速度為30cm/s,所以熱電偶受到的溫度激勵可視為一個上升時間0.4s的斜坡溫度信號。
 
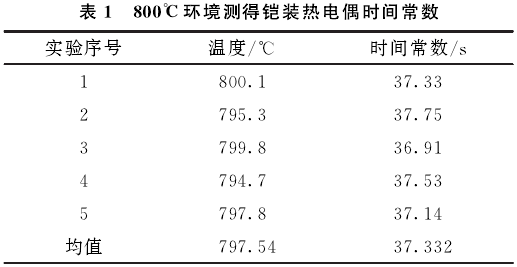
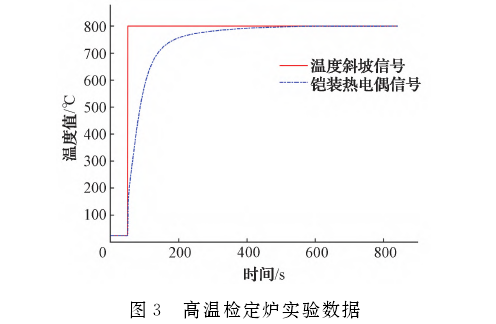
　　首先,通過溫度控制器使爐溫保持在某一較高溫度下;其次,使用上位機設定采集參數,并開始采集;再次,啟動預先設定好的傳感器快速給進裝置,將熱電偶勻速送人檢定爐內的恒溫區并保持在固定位置;最后,等待采集結束將數據保存并在上位機顯示,讀取其時間常數。依據此試驗方案在800℃實驗條件下進行5次獨立重復實驗，表1為實驗結果。計算得鎧裝熱電偶時間常數均值為37.33s,平均溫度為797.54℃，計算得靜態誤差為0.307%。第1次獨立實驗結果如圖3所示。
 
 
2基于HHO的補償算法
2.1HHO算法
　　HHO是一種新型的群體智能優化算法，由Heidari等[明于2019年提出。這種算法的設計靈感來自哈里斯鷹.群體捕食過程,其特點是采用多種狩獵策略相結合的方法,并擁有參數少,綜合性能強和收斂精度高等優點。
1)搜索階段
　　哈里斯鷹在較大范圍等待并搜索獵物,此階段會從兩種不同的行動策略中,隨機且等概率選取--種來執行。其公式如下:
 
　　式中:E0表示猜物初始逃逸能量,其取值為(-1,1)的隨，機數;t是當前迭代次數;T為總迭代次數。隨著逐次迭代,逃逸能力E的絕對值呈減小趨勢。當逃逸能量絕對值大于1時,認為獵物能量充足,此時為探索階段。當逃逸能量絕對值小于1時，認為獵物能量逐漸衰減,可以逐步包圍并捕食,此時即為開發階段。
3)開發階段
　　根據逃逸能量E及隨機數均勻分布在(0,1)的逃脫模擬參數r的大小,采取4種不同的包圍策略。當逃逸能量E較大時,認為獵物剩余能量較多,采取軟包圍,反之則采取硬包圍。當r≥0.5時認為獵物逃脫失敗,采取包圍策略捕獵，r<0.5則認為獵物逃脫成功,就可以采取俯沖方式進行包圍,調整位置。
(1)軟包圍,當r≥0.5，|E|≥0.5時,此時獵物有較多的精力逃跑,鷹群將會柔和的圍繞獵物,使其疲憊。此階段數學模型為:
 
2.2動態補償原理
　　熱電偶具有低通特性,而且工作頻帶較窄,實際測量過程中往往不能覆蓋輸人信號的所有頻率。通常的熱電偶的工作頻帶為5Hz,這意味著測量更高頻率的溫度信號時會產生幅值衰減,導致輸出波形失真，產生動態誤差，為了減小這種誤差,通常的做法是對熱電偶進行動態補償,在其之后串聯一動態補償模型,拓寬其工作頻帶、減小動態誤差并加快響應速度,示意圖如圖4所示。
　　其中x(n)表示熱電偶感受到的溫度信號，y(n)表示熱電偶的輸出信號，x'(n)表示補償后的信號。
 
　　建立動態補償模型的步驟同傳感器系統辨識方法類.似。首先,通過實驗得到傳感器的輸人輸出數據;其次,選擇適當的系統模型,以提高準確度;最后,使用參數計算算法得到補償模型的待定系數。關于動態補償模型可分為線性模型和非線性模型,線性模型的代表有傳遞函數學模型、狀態空間模型等,典型的非線性模型有神經網絡模型、Hammerstein等[13]。選擇合適的模型可有助于提高補償精度;其中,傳遞函數模型具有簡單方便、易于硬件實現和適用于單輸人單輸出問題等優點,在熱電偶補償方面被廣泛應用，本文選擇這種模型對熱電偶補償。補償系統H(z)公式如下:
 
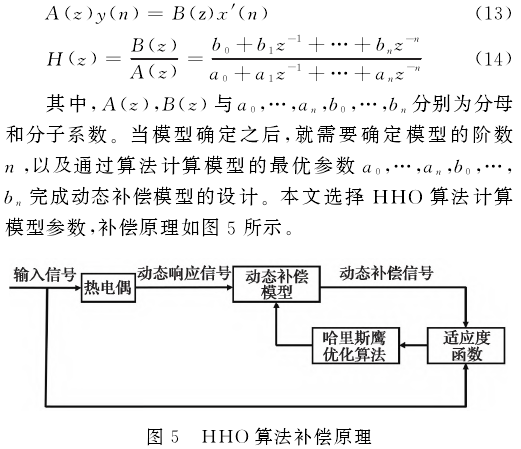
　　其中,輸入信號經過熱電偶之后,會得到失真動態響應信號;HHO算法會給動態補償模型隨機初始參數,動態響應信號通過此動態補償模型之后,同熱電偶的輸入信號一起得到適應度;HHO算法可根據適應度函數的變化,不斷尋優，調整最優的動態補償模型參數,使適應度函數最小,從而得到最優的參數,進--步得到最優的動態補償模型。
　　在動態補償方面,最小均方誤差是最常用的適應度函數,其表達式如下:
 
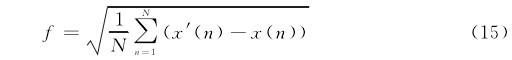
　　式中:x(n)是斜坡信號;x'(n)為動態補償之后的信號動態補償的目的之-一，就是使x'(n)更接近于x(n),兩者重合程度愈高,則代表補償效果越好。
　　為獲得更理想的補償效果,可對適應度函數做出改進。在均方誤差的基礎上增加了超調量因子以及權重系數,減少了補償后信號局部瞬時超調量。Xu等°]采用了分段式的適應度函數,以算法迭代的次數和補.償后的超調量為判斷條件，執行不同的適應度函數策略，在有效降低瞬時超調量的前提下獲得了更快的響應速度前者的適應度函數方案易于實現、效果明顯且需調節的參數較少,故使用改進后的適應度函數如下:
 
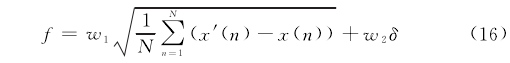
　　式中:w1、w2為權重系數;δ為補償后的超調量。取不同的w1.w2值,進行20次獨立重復實驗,選取w1、w2分別為0.8和0.2。當w2的權重逐漸增大時，超調量逐漸減小,但當權重增大到一定程度時,會導致補償后的信號第-個峰值遠小于實際溫度值的現象。實驗結果如表2所示。
 
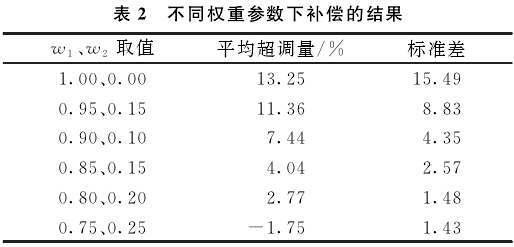
　　在相同條件下,兩種適應度函數下的超調量平均值分別為13.25%和2.77%。實驗證明，新的適應度函數可有效抑制超調量,大幅減小了瞬態誤差,其某次結果歸一化對比如圖6所示
 
　　理論.上,動態補償模型的補償效果會隨著階數增加而更好,但是當階數逐漸增加到一定數值后,補償效果的改善會越來越不明顯[4],本文選擇階數為5階。使用HHO算法,參數設置為種群數目30、迭代次數10000、空間維數12、參數范圍為-5,5]。重復運行20次,取最佳結果,得到動態補償模型的傳遞函數參數:
H(z^-1)=(4.977+2.772z^-1+0.06051z^-23.851z^-3-4.391z^-4+0.4606z^-5)/(2.934-2.307z^-1-0.07521z^-2-0.7683+z^-3+0.1623z^-4+0.08181z^-5)
　　作為對比,使用PSO算法在相同條件下進行補償運算,粒子群的自身參數設置為慣性因子w=0.8,自我學習因子與群體學習因子c1=c2=2,速度范圍[-0.8，0.8」。
　　圖7所示為兩者補償效果對比，從數據中讀出使用HHO算法將鎧裝熱電偶的時間常數從37.33s減小到了1.91s,并且到溫度達峰值的時間從478.5s減小到了4.92s,極大的提升了其響應速度。且從圖中可以明顯看出,相比PSO,HHO算法補償后的鎧裝熱電偶時間常數與到達峰值的時間都有很大提升(PSO算法補償后,鎧裝熱電偶的時間常數為3.73s,溫度到達峰值的時間為51.85s)。
 
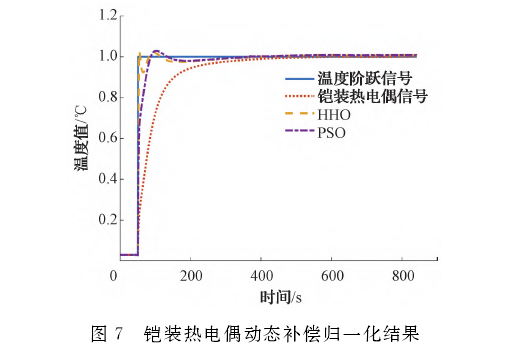
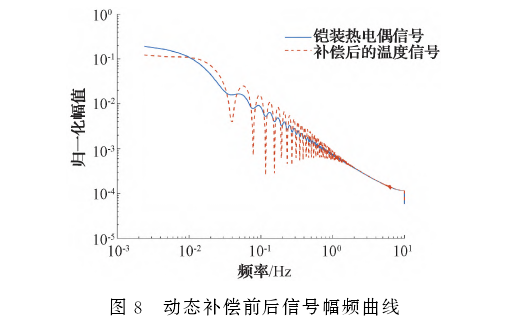
　　圖8所示為補償前后的信號頻譜圖,可以看出,經過補償后的溫度信號主要頻率分量的幅值都有所上升,尤其是較高頻的部分
 
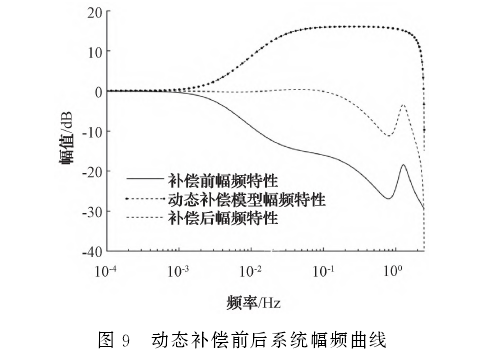
　　使用MATLAB系統辨識工具箱根據實驗數據得到鎧裝熱電偶的傳遞函數模型,并將動態補償模型串聯其后,得到補償后的系統模型。畫出補償前、動態補償模型以及補償后系統的幅頻特性曲線如圖9所示。從圖9可以看出,動態補償環節有效拓寬了鎧裝熱電偶的工作頻帶,工作頻帶從0.02Hz拓寬到了1.56Hz。但是,拓寬頻帶的同時不可避免的會帶來高頻噪聲的放大，而高頻部分的信噪比往往較低,過度的放大此部分的信號會極大影響.有效信號,所以幅值過低的高頻信號很難被恢復。
 
2.3動態補償模型驗證
　　在動態測溫實踐中,溫度信號的持續時間往往無法使熱電偶達到熱平衡,此時熱電偶的動態誤差會很大。為了模擬這種情況,使用基于高溫檢定爐的動態校準系統,使用傳感器快速給進裝置將鎧裝熱電偶送人高溫檢定爐,并使其在高溫區保持不同的時間后送出,采集多次數據。圖10所示為其中的兩次溫度與加熱時間都不同的實驗數據以及補償結果。
 
　　從圖10可以看出，鎧裝熱電偶的信號由于熱電偶自身熱慣性,在加熱結束后仍未到達熱平衡,導致測量結果誤差較大。經過動態補償后的信號能更真實的反映溫度的變化,4s左右就可到達峰值,且峰值處與真實溫度的誤差分別從46.91%、33.26%減小到2.2%.4.6%。
3結論
　　為了改善鎧裝熱電偶的動態性能,本文利用高溫檢定爐構建了一種熱電偶的動態校準系統,并利用其獲取了鎧裝熱電偶的動態校準數據以及其時間常數。其次,使用HHO算法依據實驗數據建立了鎧裝熱電偶動態補償模型,為了減少在動態補償中容易產生的大額超調量,在其中使用了改進適應度函數。實驗證明,使用此方法可將熱電偶測量系統的時間常數從37.33s減小到1.91s;超調量相比于原適應度函數從13.25%減小到2.77%,減少了79%;工作頻帶從0.02Hz拓寬到了1.56Hz。通過驗證實驗，進一步驗證了此方法可有效改善鎧裝熱電偶的動態性能，減小實際測量過程中因其動態性能不足而引起的誤差。