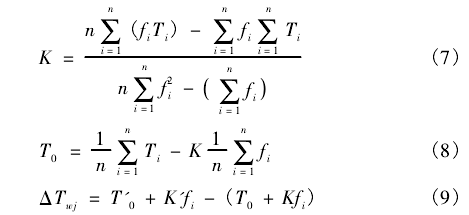基于鉑電阻傳感器的動態特性試驗

摘要:由于熱電阻測溫法的測溫精度高、穩定性好、測溫范圍廣,被廣泛應用于油田勘探開發中,但該測溫方法常因傳感器自身材料屬性的原因對測溫的實時性造成影響。該文以油田井溫測井中常用的鉑熱電阻為研究對象,根據熱力學定律,利用測井軟件warrior及多路溫度測試儀(安柏AT4204),完成了對鉑熱電阻動態響應過程的記錄,實現了實驗數據的自動采集;再利用MATLAB軟件將實驗數據進行處理,得出鉑熱電阻在不同溫度、不同直徑及不同長度下的感溫時間常數的數學模型。在保證測量精度的情況下，為以后在測井過程中優化測速提供必要的數據支持和理論指導。
0引言
　　溫度是地層重要的物理參數,也是油水井開發中井下開采層的物理特性出現變化最容易被檢測的參數。利用井溫測井得到的測井資料,就可以判斷出井筒中溫度出現異常變化的具體位置和原因,確定地層的溫度和此地的地溫梯度,并且可以了解到井內流體的具體流動狀態，劃分井下注入水層的剖面情況，完成對產層位置的確定和固井水泥的.上返高度的測量，檢查井筒壁有無竄槽情況發生，以及對井筒內管道的酸化壓裂效果的評價等工作”。在實際測井過程中，常用的溫度傳感器有熱電偶傳感器、光纖傳感器和熱電阻傳感器等,由于熱電阻傳感器的測溫精度高、測溫范圍廣、耐壓性能和抗振性能比較好，所以在井溫測量中常選用熱電阻傳感器進行實際井下測溫。而用熱電阻測量動態溫度時，熱電阻自身會有一定的響應時間，存在一定的延遲性,導致井溫測量過程中測溫點與實際地層點不相對應的問題，即井溫曲線對應深度存在誤差。
　　在實際井溫測井中通常使用鉑電阻PT100作為測溫傳感器，所以該文以鉑電阻PT100為主要試驗對象,完成對其動態響應過程的記錄,得出了鉑電阻測溫時長度、直徑與感溫時間常數之間的關系,并由此建立數學模型，即可在實際井溫測量中提供必要的理論基礎和實踐指導。
1.傳感器動態響應模型
　　在溫度傳感器的響應過程中,其表面的換熱熱阻通常情況下遠大于自身內部的導熱熱阻，因此可以認為傳感器在一-瞬間的內外溫度場是一致的。將在動態響應過程中溫度與時間看成是一元函數關系,再根據熱力學定律可以得到傳感器在流體環境下冷卻或者加熱的熱力學模型田。而在井溫測井中，可以將整個測井過程當做是傳感器的加熱過程，所以該文著重分析在加熱過程中的熱力學模型，即:
 
　　當t=Tc時,由式(3)得y=1-(1/e)=0.632.表示在溫度傳感器的整個動態變化過程中，溫度變化至整個動態過程溫度變化的63.2%時51,對應的時間差值△t就是所要求的時間常數，為此設計相關試驗求得該時間常數△t。
2試驗設計
2.1試驗設備
　　表1所示為試驗所需設備及規格型號。
 
2.2試驗系統
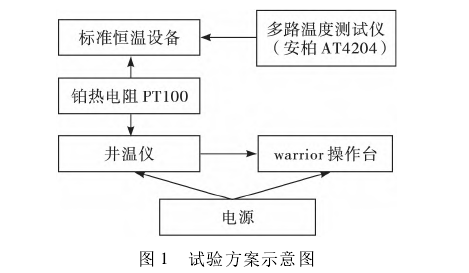
　　試驗方案示意圖如圖1所示。該試驗系統包括標準恒溫設備、鉑熱電阻PT100、多路溫度測試儀(安柏AT4204)、warrior.操作臺、井溫儀及電源。由于熱電阻的感溫時間常數與材料規格和直徑密切相.關國,該文試驗熱電阻分別選用φ2.5×30,φ2.5×35,φ2.0×35和φ2.0×45的PT100鉑電阻傳感器。
 
2.3試驗步驟
(1)傳感器的校驗
　　將恒溫設備作為溫度源,將多路溫度測試儀中的一個探頭放置于恒溫設備中，將傳感器與多路溫度測試儀中的另一個溫度探頭固定在一起，使二者頭部處于同一位置,并與之前的探頭位置保持平行，傳感器另一端與萬用表相連。啟動升溫，當恒溫設備升溫到設定溫度之。上,等待降溫至設定溫度并穩定,記錄下萬用表顯示的傳感器的阻值,每5℃記錄一次,將實驗數據與標準數據進行對比,判斷傳感器溫度阻值是否滿足線性要求切。
(2)實驗準備
　　將恒溫設備作為溫度源，設定被測溫度和采樣率，選擇接收端口,將多路溫度測試儀中的一個探頭插入恒溫設備中,啟動升溫，當恒溫設備升溫到設定溫度之，上,關閉開關，讓其自然冷卻,待溫度降至所設定溫度并穩定時，點擊warrior軟件界面上的“開始采集”按鈕.實驗開始。
(3)階躍信號的采集
　　將鉑電阻傳感器與溫度儀相連，將傳感器與多路溫度測試儀中的一個溫度探頭綁定在一起，使二者頭部處于同一位置，待溫度降至所設定溫度并穩定時，快速插入恒溫設備中，并保持其與之前的探頭位置處于同一水平位置，保證傳感器完全浸沒于硅油中,形成類似于“階躍輸入信號”，等到響應曲線保持平穩后，點擊warrior軟件界面上的“停止采集”按鈕和“保存數據”按鈕，保存實驗數據和圖像，將傳感器取出。
(4)階躍試驗
　　當傳感器自然降溫到室溫之后，分別改變傳感.器的長度和直徑以及恒溫設備的設定溫度，重復步驟(2)和步驟(3),獲得傳感器在不同的長度、直徑及溫度下的階躍響應曲線;根據實驗所得數據,在傳感器不同溫度條件下，建立時間常數與傳感器的長度和溫度之間的數學關系式以及相對誤差與長度和直徑之間的數學關系式國。
2.4線性校驗
　　根據該課題鉑電阻測試的溫度范圍,通過油浴.制造20~90℃的恒溫環境,獲得鉑電阻的阻值與環境溫度值2個數據組，根據上述實驗步驟(1)，通過MATLAB的擬合工具包中的dftool,得到溫度阻值對應的曲線以及該次擬合結果的公式、均方根誤差和回歸系數等。
　　選取φ2.0x45的鉑電阻PT100傳感器結果展示,其誤差平方和SSE為0.02567.均方差RMSE為0.04831，確定系數為1，線性程度較好，符合試驗標準。
2.5動態特性響應曲線
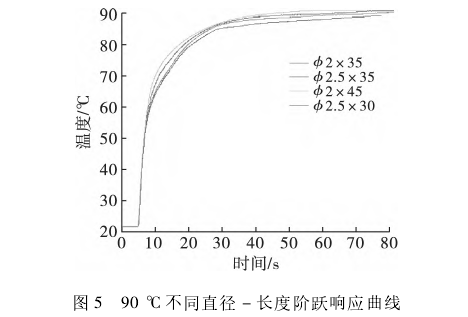
　　按照前面實驗步驟，得到直徑和長度為φ2.5x30,φ2.5x35,φ2.0x35,φ2.0x45,室溫分別為30℃.40℃.50℃.60℃.70℃.80℃和90℃時的實驗數據，建立傳感器長度-直徑與所測溫度之間的階躍響應曲線。該文選取30℃.50℃.70℃和90℃時的響應曲線進行展示,結果如圖2~圖5所示。可以看出，在不同溫度下，響應曲線整體都是呈現先劇烈上升再逐漸平緩的狀態,并且上升時間與尺寸的不同有關。
 
 
2.6穩定性誤差曲線
　　根據《中華人民共和國石油天然氣行業標[12]準一-井溫儀校準方法》2，穩定性誤差按下列公式計算。
 
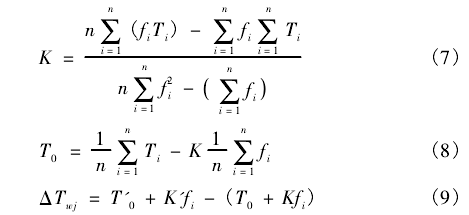
　　式中:n為測量點數;T´0為井溫儀校準前的平衡溫度,℃;K´為井溫儀校準前的儀器常數，℃/Hz;T0為井溫儀的平衡溫度，℃;Ti為井溫儀在第i校準點的實際溫度值,℃;K為井溫儀的儀器常數，℃/Hz;ƒi為井溫儀在第i校準點輸出響應值.Hz。
3數學建模
　　將實驗記錄的數據導入MATLAB軟件中,利用cftool中polynomial多項式擬合功能，進行數據插值[14]并基于最小二乘法的曲線擬合功能，得出下列數學模型。
3.1溫度為50℃時的動態響應數學模型
　　根據試驗得出的數據,建立了在不同溫度下，基于PT100的不同尺寸的動態響應數學模型。文中選取溫度為50℃時的數學模型進行展示，動態響應三維圖如圖6所示。
 
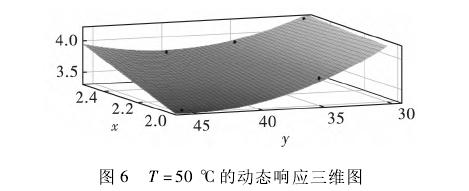
模型如下:
t=17.43-2.68x-0.56y+0.084xy+0.0044y²(10)
　　式中:x為傳感器的直徑;y為傳感器的長度;t為熱響，應時間。
　　式(10)反映出該模型在被測溫度為50℃時，傳感器的直徑與長度對其熱響應時間的影響。其中傳感器的長度對其熱響應時間的變化影響更大，而直徑對其變化影響比較小。
3.2穩定性誤差的數學模型
　　該文利用試驗所得的數據，對在試驗過程中計算得出的穩定性誤差進行了數學建模，分析討論了試驗所求的誤差及穩定性誤差的數學模型和擬合的三維曲面圖,如圖7、圖8所示。
 
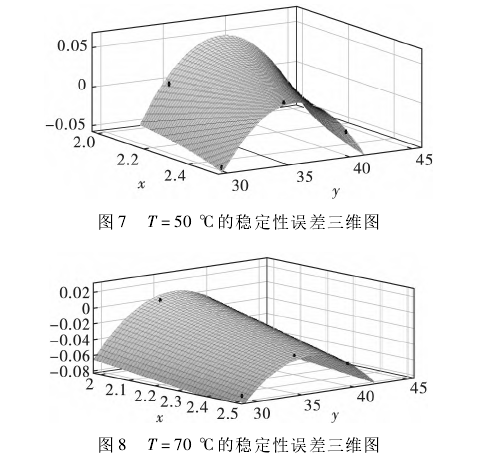
50℃時的穩定性誤差數學模型為:
t=-6.317+1.335x+0.2606y-0.03676xy-0.002373y2(11)
70℃時的穩定性誤差數學模型為:
t=-1.856+0.0891x+0.1003y-0.004511-0.00124y2(12)
　　式中:x為傳感器的直徑;y為傳感器的長度;t為不同溫度下的誤差值。
　　通過分析50℃和70℃時的穩定性誤差的數學模型，發現對穩定性誤差產生影響的因素有兩點:①傳感器的直徑與長度都對穩定性誤差有影響,其中長度對穩定性誤差的影響幅度更大,而直徑對穩定性誤差的影響程度比較小;②被測溫度對穩定性誤差也有影響，不同溫度所對應的誤差曲面趨勢圖也不同，溫度越小，模型越陡峭，溫度越高,模型越平緩。
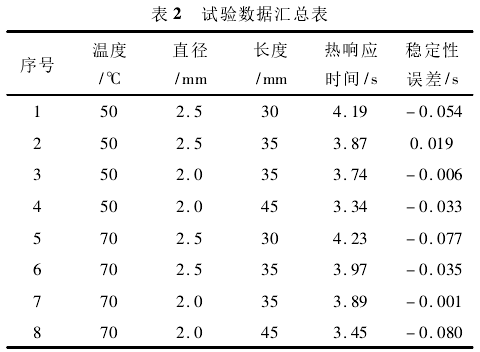
3.3驗證
　　為驗證試驗,取另外幾支PT100熱電阻做相同試驗，獲得的試驗數據見表2。將表2數據代入上述數學模型中,若符合其測量精度及誤差,說明建立的數學模型可以方便快捷地驗證所選的熱電阻的尺寸是否合理，并可以在符合自身精度及誤差的條件下，快速地得到其對應的感溫時間常數,為日后的實際井下測溫提供了一定的理論與實驗依據。
 
4結論
　　該文選取鉑熱電阻PT100為研究對象，對其在加熱過程中的動態響應這一特性進行了試驗,最終建立了其在不同溫度、不同尺寸下的動態響應數學模型。為了在實際井溫測量中提供必要的理論依據和實踐指導,基于該試驗情況給予以下結論及建議:(1)通過該文試驗數據和曲線可以看出，熱電阻的感溫時間常數與其直徑和長度有關，相同直徑下，長度越長感溫時間常數越小;相同長度下，直徑越細感溫時間常數也越小。
(2)感溫時間常數基本在3.0~4.5s之間,隨著溫度的升高，感溫時間常數的差距越小，根據傳感器的數學模型可以看出，其長度對于參數的影響更大。
(3)在實際井下測溫過程中,由于井下情況較復雜且環境較惡劣，并非傳感器的直徑越細、長度越長越好，而是應結合實際情況選擇合適的傳感器尺寸。