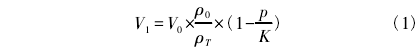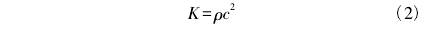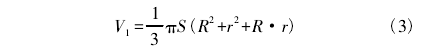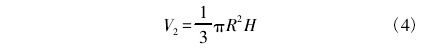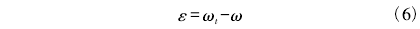溫度對不同張力下電容式壓力變送器精度影響

摘要:為提高電容式壓力變送器測量精度,溫度和中心測量膜片預加張力對其影響。采用流固耦合等效分析方法，以測量膜片位移為分析指標,通過DIC(digitalimagecorrelation)實驗驗證預加張力大小，分析20~70℃時,不同預加張力條件下測量膜片位移變化。結果表明:無預加張力時，溫度與位移為二次曲線;有預加張力時，溫度與位移為線性關系,其線性系數是-種靈敏度系數。位移相對于基準位移的位移偏移量ε隨溫度增加;預加張力增加,e減小。給定預加張力下，溫度與ε為線性關系，其系數為兩個靈敏度系數之差，給定溫度下，預加張力與ε是非線性關系，預加張力與靈敏度系數為冪函數關系。結果可為提高電容式壓力變送器可靠性提供參考。
0引言
　　工業過程檢測與控制中,壓力儀表占現場儀表的三分之一-左右“。，電容式壓力變送器作為壓力測量與流量測量儀表的核心部件,其工作原理為當外界壓力作用于隔離膜片，隔離膜片發生變形引起δ室內的傳遞介質流動，導致施加預加張力的中心測量膜片在壓差作用下產生變形位移,引起固定電極和測量膜片之間距離的變化，從而使二者電容量發生改變，電路控制部分將電容量的變化轉換成電壓的變化.生成輸出信號,利用電學方法間接測量得到壓力差值或壓力值。同時電容式壓力變送器是直接與被測介質接觸的現場儀表常在高溫、腐蝕、振動、沖擊等環境中工作。由于工藝流程的大型化、復雜化及智能化的未來發展要求,對檢測儀表的精度、穩定性、可靠性提出了更高的要求。據相關表明,我國自行研發的中高檔儀器儀表的性能參數已與國外產晶十分接近,但.受制于工業性能測試評估體系的缺失，導致影響儀表可靠性的指標尚不明確,無法評估儀表的可靠度,有可能出現故障漏報和誤報現象,因此,在綜合電容式壓力變送器儀表的三大誤差影響精度因素的基礎上印。
　　分析溫度和測量膜片預加張力對于電容式壓力變送器測量精度的影響。對于電容式壓力變送器測量精度的溫度影響,已經有一系列的相關分析。分析了電容式壓力變送器的綜合誤差主要由儀表本身的測量精度A,環境溫度變化帶來的誤差T以及靜壓變化帶來的誤差S3部分構成。由此可見，環境溫度變化對于變送器的測量精度的影響不容.忽視。使用電容式差壓變送器測量時，需要對溫度誤差進行補償或校正，減少其對測量精度的影響。說明了電容式壓力變送器δ室內的傳遞介質會隨溫度變化從而對測量精度產生影響,這是溫度誤差產生的一個主要因素。電容式壓力變送器實際使用情況下的各類故障,存在由于測量介質溫度過高導致膜盒組件靠近測量端側的δ室內的傳遞介質膨脹導致儀器儀表損壞的實例。在實際情況中,存在由溫度引起的電容式壓力變送器的零點漂移誤差，并且漂移誤差會隨溫度變化而變化。說明了壓力變送器如何選擇溫度電阻，通過溫度補償電路進行溫度誤差的補償。由于是通過3個溫度點來進行溫度電阻的選擇，溫度電阻的選擇方法簡單,調節范圍有限，很容易因為溫度電阻選擇不恰當導致壓力測量不準確。針對差動平行極板初始極距不同的問題進行誤差分析，得到一種誤差校正方法。等分析了電容式雙動極板的結構特性,發現其線性范圍提高,降低了非線性范圍。
　　盡管目前針對電容式壓力變送器的溫度影響因素眾多，但是這些分析與結果大多是聚焦于單純的溫度變化及其補償,對于電容式壓力變送器內部結構部件耦合溫度影響分析涉及不多。事實上，通過電容式壓力變送器的工作原理可知,其內部構件測量膜片的預加張力對于溫度誤差也有十分重要的.影響。通過對電容式壓力變送器工作原理的分析得到電容式壓力變送器是由測量環節和轉換.環節構成開環結構設計,雖然結構簡單,但是由于開環,各個環節的誤差會按照1:1的關系傳遞到后級。分析了電容薄膜真空計的感壓膜片的預加張力與位移的關系，其在不同預加張力作用下受到不同壓力載荷產生的位移變化是不同的。因此測量膜片結構參數的改變疊加上溫度誤差，會對整機性能產生不可忽視的影響。
　　已有基礎上，對某電容式壓力變送器通過DIC(digitalimagecorrelation,數字散斑相關法)實驗反求其內部測量膜片的預加張力,然后采用液體熱膨脹的流固耦合等效分析方法"對不同預加張力條件下的測量膜片的溫度-位移進行數值模擬。.在此基礎上分析測量膜片位移變化和相對基準位移的位移偏移量?隨溫度和預加張力的變化規律。
1計算方法與模型
1.1計算方法
　　主要電容式壓力變送器膜盒的測量膜片在不同預加張力條件下,由于膜盒兩側的δ室溫度.分布不均勻，導致溫度較高的δ室內的傳遞介質產生溫度膨脹，分析20~70℃的溫度變化對其測量精度的影響。利用等效表面載荷的方法并結合液體溫度、壓強和體積之間的關系，設定在電容式壓力變送器膜盒中，溫度升高導致的傳遞介質膨脹對于膜盒的作用是均勻分布的,傳遞介質為不可壓縮流體,不需要考慮傳遞介質的黏度隨溫度變化情況以及流動阻力。在隔離膜片和中心測量膜片的彈性變形內，隔離膜片和中心測量膜片的受力決定了其變形的大小，將液體模.型的溫度膨脹變化等效為壓力變化,省去液體分析模型。通過逐漸加大壓力來模擬溫度升高的效果,控制方程的計算表達式為
 
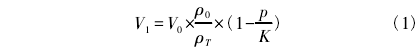
　　式中:K為液體的體積模量;ρ0為初始溫度下液體的密度;p為在容器內壁施加垂直于內壁表面且處處相等的壓力;V0與V1分別為變形前和變形后的體積:ρT為各參數代入PVT公式后求得的等效液體的密度。通過對比液體在不同溫度下的密度分布,可得到此時等效液體的溫度T。
　　甲基硅油體積模量滿足式(2):
 
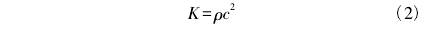
　　式中:ρ為甲基硅油密度;c為甲基硅油體積聲速。
1.2膜盒建模
　　以某款實際型號的電容式壓力變送器為例,通過對其進行結構拆分并結合工作原理分析,其主要由結構部件和電路部件構成。膜盒是其核心結構部件。圖1為膜盒工作原理示意圖,圖2為膜盒結構示意圖。膜盒由兩側相同的波紋隔離膜片,中間為施加預加張力的中心測量膜片和2個相同的半杯體構成。其中半杯體由陶瓷體、玻璃體和半杯體殼體組成,三者在具體的膜盒結構中被加工組成一個結構整體,因此在膜盒仿真分析中視為一個整體參與仿真分析。膜盒內部的傳遞介質為甲基硅油液體,儲存在由隔離膜片，半杯體和中心測量膜片三者共同構成的密封的δ室內,δ室容積為2mL,兩側各一。
 
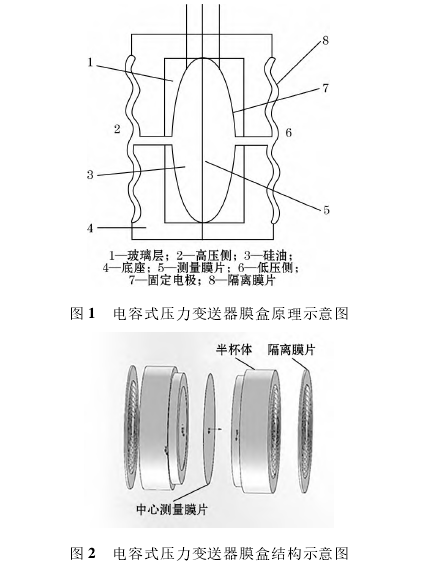
　　通過對膜盒的結構拆解及工作原理的分析,結合主要問題及分析方法,確定主要分析部件為波紋隔離膜片,中心測量膜片以及傳遞介質。據此對結構進行簡化。由于在20~70C條件下,液體的溫度變化效果遠大于金屬部件的溫度變化效果,因此將半杯體部分認為是構成液體存儲結構的一部分,不參與仿真分析。同時將膜盒結構理想化，不考慮其中金屬零部件的結構中材料的缺陷和加工過程等產生的殘余應力。
1.3仿真分析建模
　　由于利用流固耦合的等效方法分析，流體模型可以進行等效處理,因此對固體結構部分進行建模。表1為膜片材料的力學性能參數表,表2為波紋隔離膜片的型面參數表。波紋隔離膜片的直徑為30mm,厚度為0.05mm,波紋采用正弦波形，膜片材料為316L.鋼,該材料具有良好的耐腐蝕性和強度,能有效減小外部測量介質對隔離膜片的危害,延長變送器的使用時間。.
 
　　圖3為波紋隔離膜片網格劃分模型。因為波紋隔離膜片的徑向形狀是具有高度空間對稱的圓形,其徑向和軸向的寬厚比很大，采用殼單元來進行有限元分析。將模型劃分為5個部分方便網格劃分,最大網格大小控制在0.51mm,，最后經過統計得到節點數為18145個、單元數為18418個的波紋隔離膜片網格劃分模型。
 
　　測量膜片的直徑為30mm,厚度為0.1mm。膜片材料為結構鋼。因為中心測量膜片在膜盒中受到傳遞介質的保護,不直接接觸外界的測量介質，并且結構鋼屬于常用材料,經濟適用性好。結構鋼的力學性能參數如表1所示。
　　圖4為中心測量膜片網格劃分圖。由于中心測量膜片的徑向形狀是具有高度空間對稱的圓形，其徑向和軸向的寬厚比很大,利用同樣的方法進行處理。采用自動網格劃分技術,最大網格大小控制在0.5mm,最后經過統計得到節點數為3476、單元數為3401的中心測量膜片網格劃分模型。
1.4邊界條件設定
　　由于實際情況下，電容式壓力變送器的中心測量膜片具有預加張力。因此參考孟岳[10]分析電容薄膜真空計和任鳳琴[13)的熱脹式膜片張緊裝置原理,在仿真中通過對中心測量膜片施加一個徑向位移來等效代替預加張力,利用傳遞介質熱膨脹應力分析的等效.方法將溫度變化導致的膜盒一側的δ室內的液體膨脹效果等效為膨脹壓力,將膨脹壓力作為均布載荷施加到中心測量膜片一側，另一側相對取零。同時為了提高計算的精度，減小非線性誤差,打開靜力學分析模塊的大變形功能。
 
2預加張力反求
2.1DIC實驗
　　DIC(digitalimagecorrelation)是一種非接觸式的用于全場形狀、.變形、運動測量的方法,它直接處理的對象是具有一.定灰度分布的數字圖像(散斑圖),通過對比材料或者結構表面在變形前后的散斑圖,運用相關算法得到全場位移和應變。該方法對實驗環境要求極為寬松,并且具有全場測量、抗干擾能力強、測量精度高等優點。
　　DIC實驗方法:為了模擬膜盒受到外界測量介質.的液體壓力,采用彈簧、硅橡膠和旋轉抓馬構成壓力施加設備，通過壓力計算公式結合彈簧剛度系數等參數計算位移,可以實現旋轉抓馬的不同位移來模擬液體不同壓力的施加情況。對膜盒一側(設定為A側)波紋隔離膜片施加模擬壓力0.2MPa,采用DIC設備，分析另一側(設定為B側)波紋隔離膜片的變形位移情況。具體實驗流程和實驗現場如圖5、圖6、圖7所示。
 
2.2DIC實驗結果分析
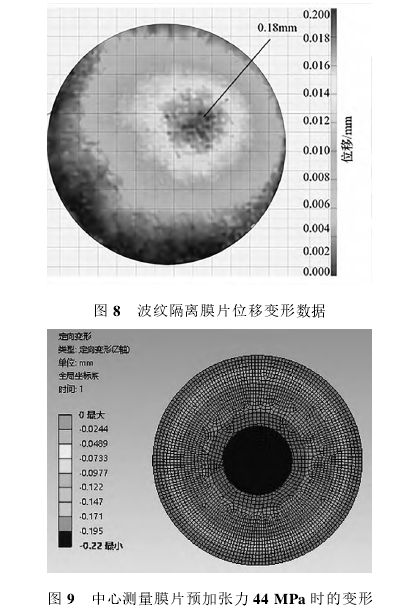
　　圖8為通過DIC實驗得到的B側波紋隔離膜片的位移變形數據圖。圖9為通過仿真分析得到的中心測量膜片的變形結果。分析數據得到如下結果:B側波紋隔離膜片最大位移處為中心處，波紋膜片最大位移約為0.18mm。
 
　　當A側隔離膜片的變形導致δ室內的傳遞介質產生流動,傳遞介質傳遞壓力使中心測量膜片產生變.形，按照同樣的作用方式分析可得，壓力最終傳導到另一側B側波紋膜片,使其發生變形。利用傳遞介質液體的不可壓縮性條件,于是B側波紋隔離膜片變形前后容積變化V1等于中心測量膜片變形前后容積變化V2。采用容積公式簡化計算波紋隔離膜片在小變形條件下的容積變化:
 
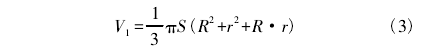
　　式中:S為波紋膜片最大變形位移;R為波紋膜片最大變形半徑;r為波紋隔離膜片中心硬芯處半徑。
　　利用容積公式簡化計算平膜片在小變形條件下的容積變化:.
 
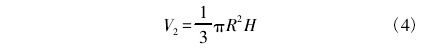
　　式中:H為中心測量膜片最大變形位移;R為中心測量膜片最大變形半徑。
　　通過小變形位移計算公式可以得到V和V2,結合流體不可壓縮條件,利用V1=V2,經過計算得施加某預加張力的中心測量膜片在0.2MPa壓力下的位移應該在0.22mm左右。表3為中心測量膜片在不同預加張力條件下的仿真分析結果,最終得到了在施加給中心測量膜片預加張力44MPa時，中心最大位移為0.19mm,符合相關實驗結果和分析數據，如圖9所示。由此建立了完善的中心測量膜片的參數信息。
 
3結果分析
3.1預加張力為44MPa時，不同溫度下的位移變形分析
　　利用DIC實驗得到中心測量膜片的實際預加張力為44MPa,結合計算分析方法,通過軟件進行仿真,分析-~側δ室內的傳遞介質在20~70℃條件下,另一側相對溫度不變時,傳遞介質溫度變化引起測量膜片.的位移變形情況,得到不同溫度下的測量膜片中心位移數據。將20℃的位移變化設定為0,并列出如表4所示的以10℃為增量,20~70℃的位移變化表。同時得到擬合公式(5)。
 
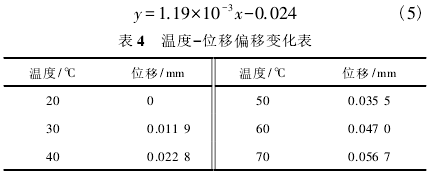
　　由表4和式(5)可見，預加張力44MPa條件下的溫度-位移變化成線性關系,斜率為1.19x10^-3。以測量膜片位移作為分析度量指標，以預加張力44MPa,20℃條件下的位移作為基準位移,分析溫度對位移偏移影響,結合表4數據和式(5)可知,每10℃的溫度變化，會引起大概1.19%的位移偏移。說明擬合公式的斜率可以作為偏移影響的一-種度量,同時說明溫度的大范圍變化會導致較大的影響。
3.2不同預加張力、不同溫度下的位移變形分析
　　前文分析的是固定預加張力下、同溫度的位移變形，在此基礎上，通過調整預加張力的大小,進一步預加張力和溫度變化對于測量膜片的影響。將預加張力以44MPa為參考，分別取預加張力為0、18、26、53、70、88MPa加以分析,圖10與表5分別是在分析一側δ室內的傳遞介質在20~70℃的條件下對中心測量膜片產生的位移變形后，得到的溫度-預加張力-位移圖以及擬合數據得到的擬合公式表。同時建立如圖11和表6所示，以10℃為增量,20~70℃的每種預加張力情況下測量膜片位移相對于預加張力44MPa條件下的基準位移的偏移分布表和偏移分布圖。選用位移偏移量ε分析位移精度情況。
 
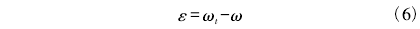
　　式中:?t,為某預加張力條件下某溫度對應的位移量;?為預加張力44MPa條件下與?t,相同溫度對應的位移量。
 
 
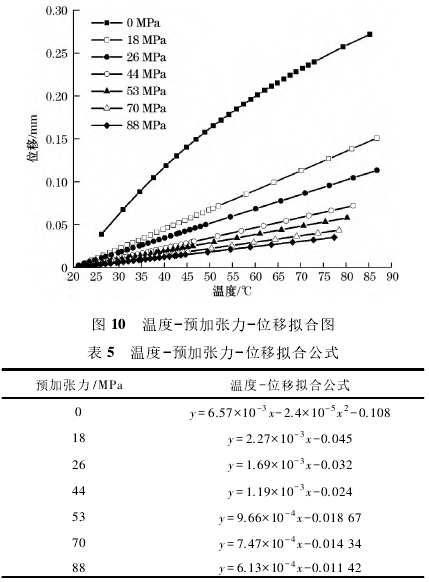
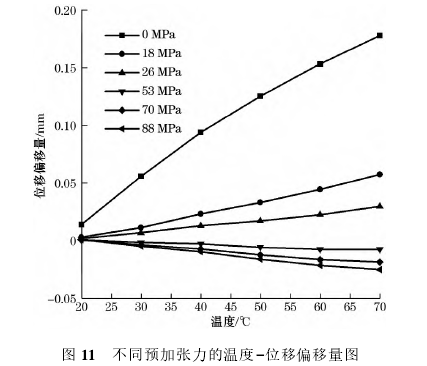
　　通過表5和圖10可見，預加張力為0MPa的測量膜片的溫度-位移變形擬合公式為二次多項式形式，預加張力不為0MPa的測量膜片的溫度-位移變形擬合公式都近似為線性關系,二者明顯不同，說明給定.預加張力可以讓測量膜片的溫度-位移變形具有線性.關系。線性關系對于后續的溫度位移偏移的處理十分有利。
　　由于不同的預加張力對應著不同的線性關系，也對應著不同的線性系數,結合線性系數的數學意義以及實際物理背景,線性系數可以認為是度量給定預加張力情況下測量膜片的溫度-位移的一種靈敏度系數。因此預加張力的合理選擇在測量膜片的設計和使用中十分重要。
 
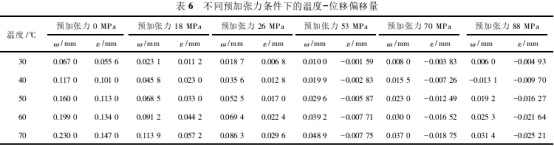
　　表6和圖11說明初始位移偏移相對來說較小，但是隨著溫，度變化的增大，偏移的效果越來越明顯,其中無預加張力情況和有預加張力情況在相同溫度變化下引起的測量膜片位移變化十分明顯。
　　當給定預加張力時,對溫度和位移偏移數據進行分析并擬合,得到溫度和位移偏移量的變化是線性關.系，相關結果如表7所示，可以認為其中擬合公式的線性系數是溫度-位移偏移量的一個度量指標，通過公式推導和數據分析，發現這個度量指標可以認為是上文中提到的給定預加張力與基準預加張力的兩個溫度-位移的靈敏度系數之差。
 
　　圖12為預加張力與位移偏移量的關系,當給定相同溫度時,對預加張力與位移偏移量數據進行分析，發現隨著預加張力的增大,位移偏移量隨之減小，但是這種位移偏移量變化不是線性關系。當施加預加張力大于基準預加張力后，位移偏移量為負數，說明由于預加張力過大，導致位移變化量相較于基準量降低,實際表現為顯示壓力數值小于實際壓力數值。
 
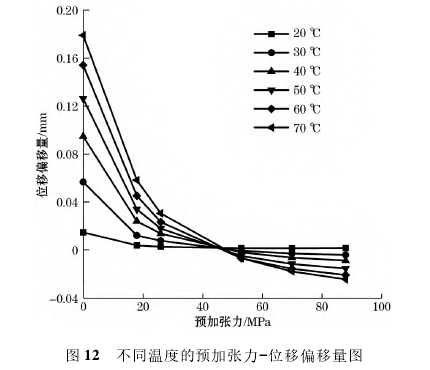
3.3預加張力與線性系數的分析
　　圖13為預加張力與擬合公式線性靈敏度系數的關系,得到擬合公式為式(7)
 
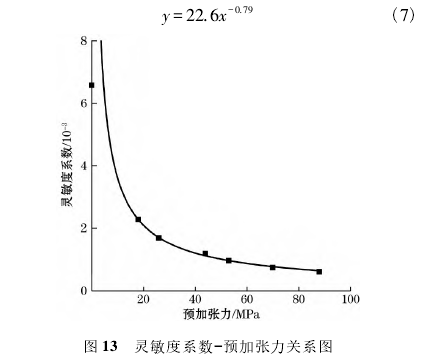
　　預加張力與靈敏度系數是一-種冪函數關系，隨著預加張力的增大，剛開始的靈敏度系數的降低是十分迅速的，但是后面靈敏度系數的降低十分有限，因此不能單純通過調整預加張力來滿足測量膜片對于不同靈敏度要求以及誤差控制的要求,還需要其他的控制手段來實現實際使用要求。結合前文中對于給定預加張力情況下的溫度-位移和溫度-位移偏移量分析,可以得出，預加張力和溫度對于位移的影響在于預加張力決定了位移變化的趨勢;溫度決定了位移變化的大小。
4結論
　　通過對電容式壓力變送器膜盒結構進行溫度與預加張力分析,得到如下結論:
(1)無預加張力條件下，溫度與測量膜片位移變化為二次曲線關系，有預加張力條件下，溫度與測量膜片位移變化為線性關系。良好的線性關系能方便后續的溫度-位移變化的處理,并且線性關系的系數可以認為是給定預加張力下的溫度-位移變化的靈敏.度系數。
(2)隨著預加張力的增加，溫度影響的位移偏移量ε明顯降低。當預加張力固定時，溫度與位移偏移.量ε還是線性關系,此時的線性關系的系數可以認為是偏移量ε的度量,實際是兩個溫度-位移變化的靈敏度系數之差。但當溫度采取某一定值時,預加張力與位移偏移量ε的關系不是線性關系。
(3)預加張力與線性靈敏度系數的關系為冪函數關系，開始時預加張力的微小改變會引起靈敏度的巨大變化,但是隨著預加張力的增加,靈敏度的改變十分有限。預加張力決定了位移偏移量的趨勢,溫度決定了位移偏移量趨勢的大小。