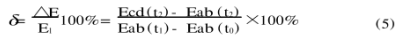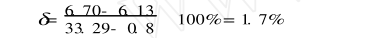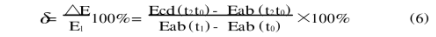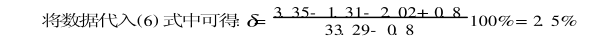熱電偶測溫的兩個實際問題的誤差分析
發布時間:2024-01-22
瀏覽次數:
摘要:論述用三線補償測溫系統,克服用
熱電偶測溫時,因冷端溫度高于100℃,或
補償導線與熱電偶不配套時產生測量誤差的原理。
1.兩個實際問題
用熱電偶測溫時,不同型號的熱電偶應配與之相應的補償導線,同時還要求熱電偶和補償導線的連接點即熱電偶冷端的溫度小于100℃。這樣補償導線的熱電特性才能與熱電偶的熱電特性一致從而才有將熱電偶冷端延伸到溫度恒定的地方的可能可是在我們工作中常常遇到這樣兩個問題:(1)隨著工業的發展冷端溫度高于100℃的場合E屢見不鮮并且很難將其溫度降低例如,高溫加熱爐隧道窯上部安裝的熱電偶;(2)補償導線型號與測溫熱電偶的型號不符合,例如庫存補償導線型號不全或一時缺乏某一型號但又不能即時解決;或使用新研制的熱電偶手里根本就沒有與之匹配的補償導線。
顯然,對于這兩個實際問題,按照通常的補償導線方法是不能夠把冷端延伸到溫度恒定的地方的,結果會給測量帶來的誤差,因此有考慮別的方法的必要。
2誤差分析
從理論角度歸納起來.上述兩個實際問題就是一個問題,即熱電偶和補償導線的熱電特性不一致為分析方便起見我們首先看正常情況下(即冷端溫度小于100℃且補償導線與熱電偶相匹配)測溫回路(圖1)的總電勢
E1=Eab(t1)+Ebd(t2)+Edc(t0)+Eca(t2)
因a和c、b和d熱電特性一致所以Ebd(t2)=0;Eca(t2)=0;Edc(to)=Eba(to)=-Eab(to)
從而可知回路總電勢為
E1=Eab(t1)-Eab(to)(1)
當冷端溫度高于100℃或熱電偶與補償導線不相配時,a和c、b和d的熱電特性就不一致從而在測溫回路(圖2中的總電熱為
E2=Eab(t1)+Ebd(t2)+Edc(t0)+Eca(t3)=Ea(t1)-Eb(t1)+Eb(t2)-Ed(t2)+Ed(t0)-Ec(t0)+Ec(t3)-Ea(t3)
從而E2=Ea(t1t3)+Eb(t2t)+Ec(t3t0)+Ed(t0t2)=Ea(t1t3)-Eb(t1t2)+Ec(t3t0)-Ed(t2t0)
若(t2)=(t3),則原式為E2=Ea(t1t2)-Eb(t1t2)+Ec(t2t0)-Ed(t2t0)=Eab(t1t2)+Ecd(t2t0)
=Eab(t1)-Eab(t2)+Ecd(t2)-Ecd(t0)(2)
比較(1)式和(2)式可得
E2-E1=Eab(t1)-Eab(t2)+Ecd(t2)-Ecd(t0)-Eab(t1)+Eab(t0)=Eab(t0t2)+Ecd(t2t0)=Ecd(t2t0)-Eab(t2t0)(3)
下面按上述兩實際問題討論其誤差。
2.1熱電偶型號和補償導線相匹配,但冷端溫度大于100℃。
此時(3)式可寫成△E=E2-E1=Ecd(t2)-Ecd(t0)+Eab(t0)-Eab(t2)
因為在100℃以下a和c、b和d的熱電特性一致的,所以Eab(t0)-Ecd(t0)=0,因此
△E=E2-EI=Ecd(t2)-Eab(t2)(4)
在同一溫度下,補償導線c.d組成的熱電偶的熱電勢總比熱電偶a.b的熱電勢大所以(4)式總是大于0,因而指示偏高。這時所帶來的誤差按下式計算,
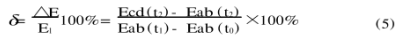
例1一支鎳鉻鎳鋁熱電偶與它所相配的銅康銅補償導線組成測溫線路,接點溫度t2=150℃,被測溫度t1=800℃,to=20℃,問它同接點溫度小于100℃比較誤差有多大?
解從BU2分度表查得Eab(t1)=3329mV,Eab(t0)=0.8mV,Eab(t2)=613mV,
從銅康銅分度表查得Eed(t2)=670mV
將數據代入(5)式可得
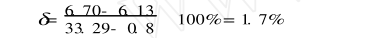
照此計算即使t1達到最高限1300℃,Eab(t1)=5237mV也會有11%誤差。若冷端溫度提高200℃,t1仍為800℃,這時誤差可以達到3.3%,t為1300℃誤差也為22%。當然被測溫度若更低誤差就更大了。
2.2熱電偶同補償導線不相四配,但冷端溫度小于100℃
這種問題的誤差由下式決定
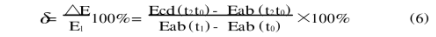
由式(6)可知,分析誤差時要注意什么樣的補償導線配什么樣的熱電偶。例如若熱電偶是EU2而配的補償導線是銅鎳銅(本是配LB;的),則Ecd(t2t0)<Eab(t2t0),AE為負,指示偏低若配的鎳鉻-考銅補償導線,(本是配ea2)則Ecd(t2t0)>Eab(t2t0),Ae為正指示偏高。
例2一支EU2熱電偶,由于庫存沒有與之相配的銅康銅補償導線,就用鎳鉻考銅補償導線代替,設被測溫度t1=800℃,冷接點溫度t2=50℃,室溫to=20℃,問它同配銅康銅補償導線比較誤差有多大?
解從EU2分度表查得Eab(t)=33.29mV,Eab(t0)=08mV,Eab(t2)=202mV,
從EA2分類表查得Ecd(t2)=3.35mV,Ecd(t0)=1.31mV
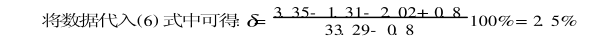
由此可見上述兩個實際問題所帶來的誤差很大的,用通常的方法是無法真實測量溫度的。
3三線補償法.
由(2)式可知,要想閉合回路的總電勢E2和溫度t1成一對應的關系,就必須使t2恒定不變同時要確切知道t1的大小,就必須進行冷端溫度校正要校正就得知道t2的具體數值。要恒定t2顯然是不可能的,而且t2的大小除非另用一支熱電偶測量,否則無法得知這就是說盡管測得了E2,用(2)式還是無法決定被測溫度ti的大小的。是否能設法把(2)式變成既不要求恒定t2;又知道t2的大小且測量線路,又很簡單呢?回答是肯定的。根據熱電偶的基本性質[2],把(2)式設計成圖3的三線補償導線電路,就能達到解決上述問題的目的。
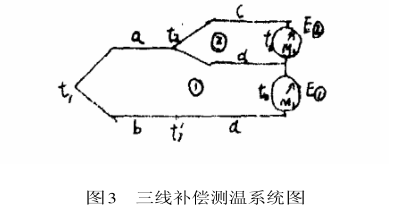
在圖3中,假定bd和cd兩接點的溫度是相同的,即都為t20在回路①中的總電勢為
E0=Eab(t1)+Ebd(t2)+Edd(t0)+Eda(t2)=Ea(t1)-Eb(t1)+Eb(t2)-Ed(t2)+Ed(t0)-Ed(t0)+Ed(t2)-Ea(t2)
故E0=Ea(t1t2)-Eb(t1t2)=Eab(t1t2)=Eab(t1)-Eab(t2)
在回路②中的總電勢為E②=Ecd(t2)-Ecd(t0),E①+E②=Eab(t1)-Eab(t2)+Ecb(t2)-Ecb(t0)
(7)式和(2)式是完全一致的,應用圖3線路測量E①和E②,并通過冷端溫度校正就可以很方便地求得被測溫度t1來決定t1的步驟是這樣(1)測量E②,加上已知t0(一般為室溫)的熱電勢Ecd(t0)得到Ecd(t2),查其分度表得到溫度t2.
(2)測量E①,用t2查出Eab(t2),加上E①得到Eab(t1),查其分度表得到t1被測溫度。
例3E知ab為EU2,cd為EA2,室溫t0為20℃;測得E②為993mV,E①為37.33mV,求被測溫度t1?
解從EA2分度表查得Ecd(20℃)=1.31mV
所以Ecd(t2)=E②+Ecd(to)=9.93+1.31=11.24mV
用1124mV查EA2分度表得t2=157"C,從EU2分度表查得Eab(t2)=641mV
故Eab(t)=Eo+Eab(t2)=37.33+641=43.74mV,用43.74mV查BU2分度表得t1=1064℃
由此證明,用三線補償法,擴大了熱電偶冷端溫度范圍,使熱電偶用于冷端溫度高于100℃的場合
測溫成為可能同時,用三線補償法,使任何型號的熱電偶,可以用一種補償導線,簡化、節省了各類補償導線的儲備,具有實在的經濟意義。
4.幾個有關問題證明
(1)在分析過程中設ab熱電偶正負兩冷端要保證同一溫度,根據現場安裝提供的條件設計各種型式的金屬套管,把兩點放在同一溫區內,使這一小段熱電偶的溫度場達到平衡。
(2)根據在熱電偶回路中接入第三種材料的導線,只要第三種導線的兩端接點溫度相同第三導線的引入不會影響熱電偶的熱電勢的這一性質cd熱電偶的熱端(即和a相接點可以任意焊接.
(3)為實用和經濟起見,cd選EA2為宜。
(4)第三根補償導線可以和d相同,也可以和c相同.
(5)熱電偶老的分度號為LB3,EU2;EA2,新的對應分度號為S,K,E.