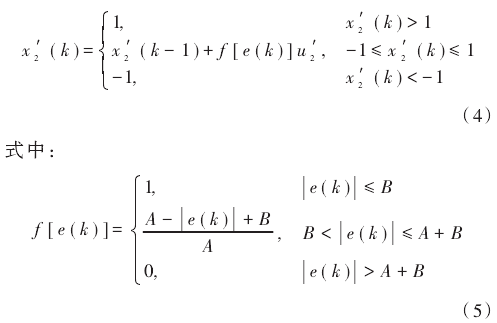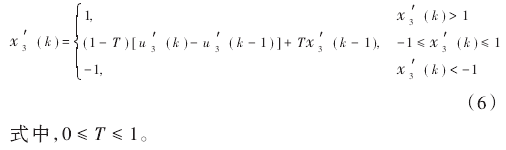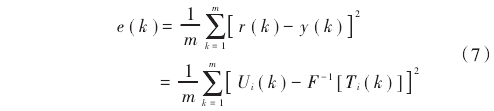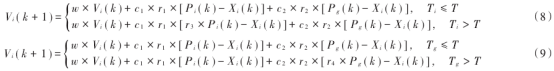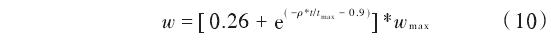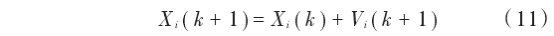PID神經網絡算法對K型熱電偶非線性校正
發布時間:2023-10-11
瀏覽次數:
摘要:針對火箭發射場發射效應測溫系統中
K型熱電偶存在的非線性特性,設計中將非線性特殊點作為訓練樣本,采用新型動態PID神經網絡算法對熱電偶進行非線性校正。針對基本BP算法收斂慢、易陷入局部極值的缺點,提出利用粒子群算法來改進網絡的尋優過程,并在傳統算法基礎,上對其慣性權值的遞減式子進行改進。使用Matlab建模仿真表明,改進算法在尋優過程中,收斂速度快,全局尋優能力強,有較好的控制效果。擬合出的溫度電壓關系呈現好的線性度,相對誤差均控制在1%以內,提高了系統測試精度,滿足對火箭發射時溫度環境效應的監測要求。
0引言
熱電偶自身的物理特性致使其輸出的熱電勢E與溫度t之間存在非線性關系,針對目前測試系統的寬范圍、精度高測量需求,需要減少非線性測量誤差。K型熱電偶的非線性校正方法有查表法、多項式擬合法、PID神經網絡法凹。其中,查表法使用大量數據,極易受到存儲容量的限制;最小二乘法以T=d0+d1E+d2E²+...+dnE
n形式擬合,在高溫階段誤差較大。針對以上問題,采用基于粒子群算法的PID神經網絡算法對K型熱電偶進行非線性校正,同時系統具有PID控制的快速輸人/輸出動態特性。
1測溫系統分析及校正原理
如圖1所示,溫度采集系統包括K型熱電偶、變送器、采編器及測控計算機。在溫度采集系統中,針對ADC誤差、傳輸線路誤差、調理和輸人跟隨誤差,設計采集存儲模塊,其由電流轉電壓模塊、抗混疊濾波器模/數轉換模塊、FPGA控制模塊,FLASH模塊組成;經變送器將電壓信號轉換成幅度為4~20mA的電流信號進行傳輸,抵抗惡劣環境干擾。而對于傳感器誤差,在實際應用中即使經過冷端補償,熱電偶測溫時冷端也很難保持為0℃。
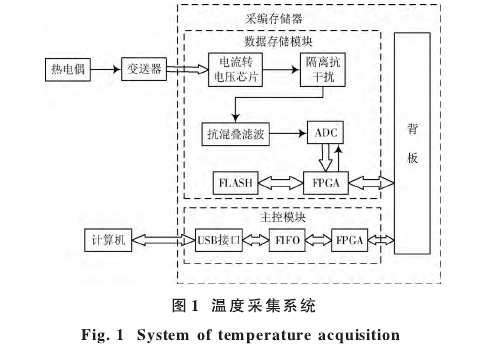
需對其線性校正,采用PID神經網絡算法校正原理如圖2所示。

2基于粒子群算法的PID神經網絡非線性校正
2.1PID神經網絡理論:
傳統神經網絡中神經元僅具有靜態的輸人/輸出特性,若用它構成控制系統時必須附加其他動態部件凹。PIDNN以PID控制器的形式定義網絡隱含層,其隱含層包括比例元、積分元和微分元三個神經元,采用粒子群算法調整權重值,反復進行學習和訓練,使目標函數達到最優甲。根據網絡輸出值的不同,PIDNN分為單輸出PIDNN(SPIDNN)和多輸出PIDNN(MPIDNN)旦,本文采取單輸出方式。
2.2溫度控制系統建模
2.2.1訓練樣本數據獲取
在實際運用中,本設計中所要測量溫度范圍是0~1300℃,所以在選擇訓練樣本時選取熱電偶分度表中的特殊點,避免數據量過大造成浪費,同時節省了計算時間。圖3為典型的熱電特性曲線圖,橫坐標表示溫度T,縱坐標表示熱電勢E。
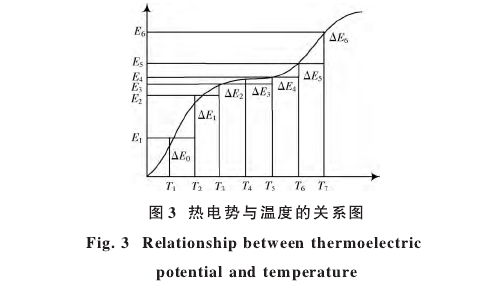
圖3中二者明顯呈現出非線性關系。選取特殊點時,首先對T等間距取值,通過分析E變化情況即△E值便可找到特殊點。令△Zi=△Ei-△Ei-1,取正數a作為門限值,當|△Zi|<α時將該點領域內近似為線性,當△Zi|≥α時則可判斷該點發生突變,即(Ti,Ei)作為特殊點。
表1為溫度在0~1300℃范圍內選取的突變點,突變點對應的K型熱電偶分度表數據作為訓練樣本。

2.2.2PID神經網絡的建立
PID神經網絡結構如圖4所示其是單輸人-單輸出的控制系統(SPIDNN),即輸人層兩個神經元,熱電偶分度表中的電壓值作為輸人r(k),?(h)代表實際輸出,y(k)為SPIDNN控制系統的實際輸出值,隱含層三個神經元,輸出層-一個神經元。
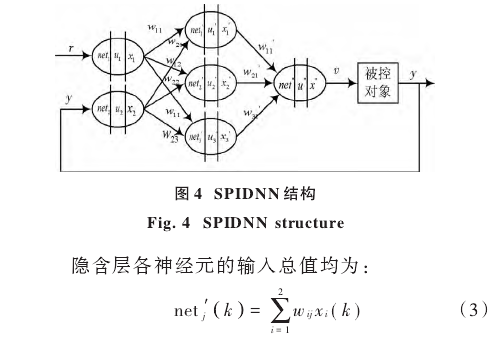
式中:j=1,2,3;wij為輸人層到隱含層的連接權重值。針對積分環節出現的積分飽和現象、微分信號引人過程中易引進高頻干擾的問題,采取變速積分和不完全微分的PID控制策略。在改進積分元中設置系數ƒ[e(k)],積分神經元輸出表示如下:
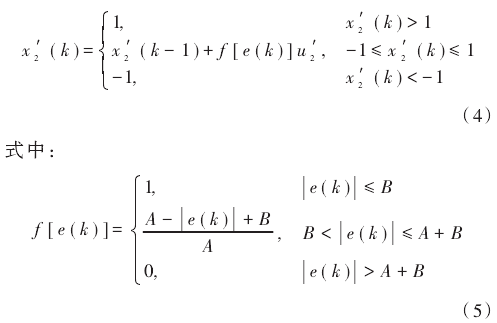
e(k)是神經網絡實際輸出與理想輸出的均方差值;A,B均為常數。當|e(k)|增大時,ƒ(h)減小;|e(k)|減小時,ƒ(k)增大。將當前輸人值加權后的和作為神經元輸出值。在改進微分元中加人了輸出自反饋的加權和,其表示如下:
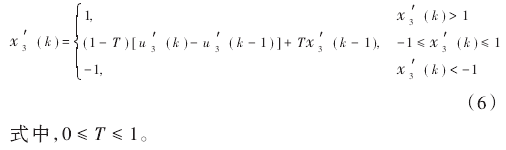
2.2.3粒子群優化神經網絡算法
使用改進的PSO算法優化權值,首先初始化所有子群粒子的速度、位置及每一子群的最優位置,性能指標函數作為適應度函數計算每個粒子的適應度值g(h)。性能指標函數為:
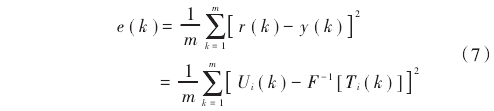
式中:e(k)是神經網絡實際輸出與理想輸出的均方差值;m為樣本數目。
然后將每個粒子的適應度與個體極值及全局極值進行比較,確定新的個體極值Pi與全局極值Pg。按照式(8)和式(9)更新速度與位置。將個體極值進化停滯步數與預設值進行比較,按照式(8)不斷更新速度,比較全局極值進化停滯步數與預設值,按照式(9)不斷更新位置。
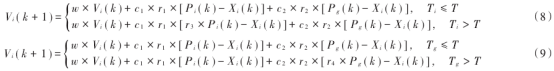
式中:Vi(h)是粒子i的速度;w為慣性權重,隨迭代次數線性遞減,保證收斂;Xi(h)為粒子所在位置;r1,r2,r3,r4是(0,1)之間的隨機數;c1,c2為學習因子;Ti為粒子i個體極值進化停滯步數;Tg為全局極值進化停滯步數,T為預設值。在慣性權值的變化過程中,采取非線性權值遞減方法,表達式如下:
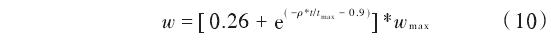
式中:Wmax為所取最大權值;t為當前迭代次數;tmax為迭代總次數;ρ為正數,根據慣性權重的范圍選取4.5。粒子按照式(11)更新自身位置:
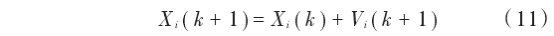
若未達到停止迭代的條件則繼續返回計算適應度值;若性能指標函數e(h)值達到期望值或者到達預設的迭代次數時,得到最優粒子,將極值賦給權值,計算結束
2.2.4仿真結果分析
初始化位置矢量X為[-0.1,0.1]的隨機數,速度矢量V為[-0.3,0.3]的隨機數;取學習因子c1=1,c2=1;慣性權重w的取值范圍是0.25≤w≤0.95;選擇種群粒子數為27;迭代次數為40。Matlab仿真結果如圖5所示。
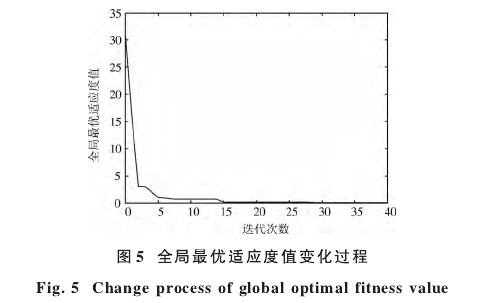
圖5是在粒子群算法進化過程中,全局最優值的適應度隨PSO迭代的變化過程可看出適應度函數在尋優過程中在第5次迭代處基本趨于0,即網絡實際輸出與理論輸出的均方差逐漸趨于0,訓練后的數據較為快速地趨于標準數據,二者間誤差較小。該過程中收斂明顯,收斂速度快且收斂性好。
慣性權重的選取對算法的收斂速度是很重要的。圖6中針對粒子群算法中的慣性權重,將傳統算法與改進算法進行仿真對比。從圖6中可看出,傳統粒子群算法過程中,慣性權值呈線性遞減,由于粒子在向群內最優位置運行時速度較快,在其到達最優點處時極有可能因為速度太快而錯過;所以在設計中使用改進的慣性權.值算法,將慣性權重按照指數的形式逐漸降低,粒子的運行速度隨著粒子與最優點間距離的減小有較為明顯的降低,保證了在尋優前期有快速收斂的能力,也確保后期有較好的收斂效果。
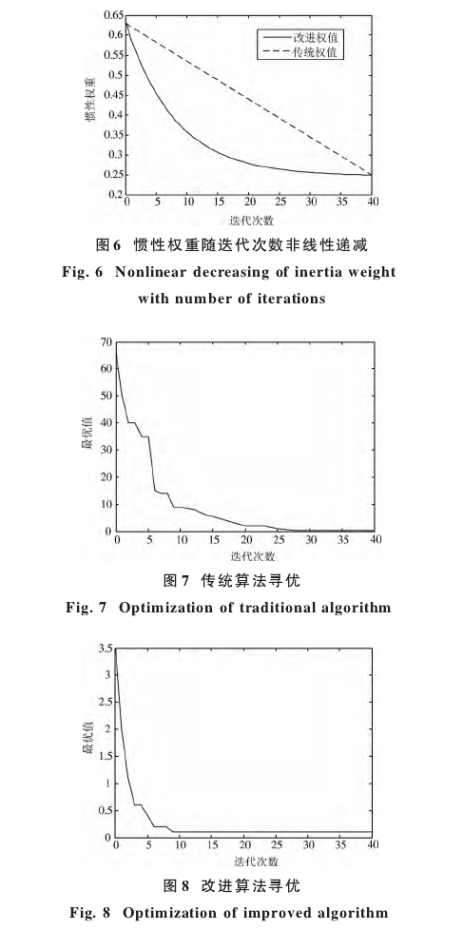
圖7與圖8分別是傳統PSO算法尋優過程和改進PSO算法尋優過程。兩圖比較,二者均可在迭代次數較小處獲得最優解,慣性權值未優化時,極易陷入局部最優。使用慣性權值優化算法時,可經過更少的迭代次數獲得最優值,易跳出局部最優點,且其在前期有較好的.收斂速度;在增強粒子局部尋優能力的同時,保證了算法的收斂性,尋優效果明顯,運行效率高;具有更強的全局搜索能力。同時優化算法的精度明顯高于傳統算法,提高了傳感器測量的可靠性和準確性。采用改進PSO算法對PID神經網絡進行仿真,解方程組得系統校正方程最優解:α0=0.1710,α1=21.6780,α2=0.0260,α3=-0.0008。在輸人溫度值一定的條件下,經神經網絡訓練后部分電壓值與標準電壓值對比結果如表2所示,可以直觀地看出誤差最小的可以達到0.1%,最大誤差控.制在1%內。訓練效果明顯得到改善。
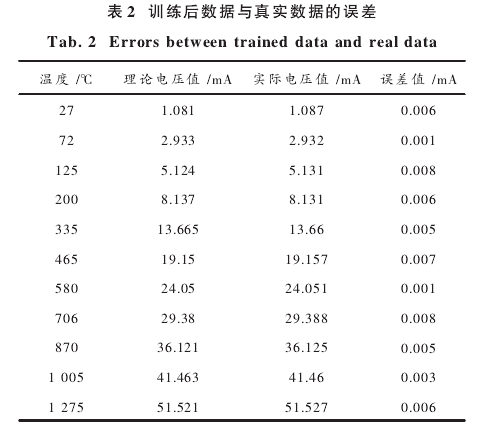
圖9為訓練后所得點與標準點擬合曲線,其中橫坐.標表示熱電勢,縱坐標表示溫度值。相比于訓練前非線.性曲線,得到明顯改善。通過神經網絡訓練后的值與標準點之間誤差很小,趨于吻合;結合PID控制方法,使得系統穩定性高,在寬范圍溫度測量過程中,溫度測量誤差一直控制在1%內,使熱電勢與溫度值呈現出較高的.線性度。

3結論
在寬范圍精度高測溫系統中,針對K型熱電偶輸出的熱電勢E與溫度t之間的非線性關系,建立PID神經網絡對其進行非線性校正,采用粒子群算法進行尋優取.值。選取E-t曲線中特殊拐點的標準值作為訓練樣本,對尋優過程中的慣性權值改進,增強其全局尋優能力。仿真結果表明:控制系統穩定性較高,正確性提高;訓練所得溫度值與標準值之間誤差均在1%以內,且二者擬合效果好,收斂速度快。正確溫度信號獲取為火箭發射塔架的健康評估提供可靠依據。